Truncated trioctagonal tiling
In geometry, the truncated trioctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one hexagon, and one hexadecagon (16-sides) on each vertex. It has Schläfli symbol of tr{8,3}. Symmetry The dual of this tiling, the order 3-8 kisrhombille, represents the fundamental domains of [8,3] (*832) symmetry. There are 3 small index subgroups constructed from [8,3] by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors. A larger index 6 subgroup constructed as [8,3*], becomes [(4,4,4)], (*444). An intermediate index 3 subgroup is constructed as [8,3⅄], with 2/3 of blue mirrors removed.
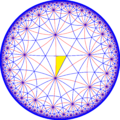
Order 3-8 kisrhombille
The order 3-8 kisrhombille is a semiregular dual tiling of the hyperbolic plane. It is constructed by congruent right triangles with 4, 6, and 16 triangles meeting at each vertex. The image shows a Poincaré disk model projection of the hyperbolic plane. It is labeled V4.6.16 because each right triangle face has three types of vertices: one with 4 triangles, one with 6 triangles, and one with 16 triangles. It is the dual tessellation of the truncated trioctagonal tiling, described above. NamingAn alternative name is 3-8 kisrhombille by Conway, seeing it as a 3-8 rhombic tiling, divided by a kis operator, adding a center point to each rhombus, and dividing into four triangles. Related polyhedra and tilingsThis tiling is one of 10 uniform tilings constructed from [8,3] hyperbolic symmetry and three subsymmetries [1+,8,3], [8,3+] and [8,3]+.
This tiling can be considered a member of a sequence of uniform patterns with vertex figure (4.6.2p) and Coxeter-Dynkin diagram
See alsoWikimedia Commons has media related to Uniform tiling 4-6-16. Wikimedia Commons has media related to Uniform dual tiling V 4-6-16.
References
External links |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||