Coxeter notation

Fundamental domains of reflective 3D point groups

, [ ] = [1] C1v	, [2] C2v	, [3] C3v	, [4] C4v	, [5] C5v	, [6] C6v
Order 2	Order 4	Order 6	Order 8	Order 10	Order 12
[2] = [2,1] D1h	[2,2] D2h	[2,3] D3h	[2,4] D4h	[2,5] D5h	[2,6] D6h
Order 4	Order 8	Order 12	Order 16	Order 20	Order 24
, [3,3], Td		, [4,3], Oh		, [5,3], Ih
Order 24		Order 48		Order 120
Coxeter notation expresses Coxeter groups as a list of branch orders of a Coxeter diagram, like the polyhedral groups, = [p,q]. Dihedral groups, , can be expressed as a product [ ]×[n] or in a single symbol with an explicit order 2 branch, [2,n].

In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson.

For Coxeter groups, defined by pure reflections, there is a direct correspondence between the bracket notation and Coxeter-Dynkin diagram. The numbers in the bracket notation represent the mirror reflection orders in the branches of the Coxeter diagram. It uses the same simplification, suppressing 2s between orthogonal mirrors.

The Coxeter notation is simplified with exponents to represent the number of branches in a row for linear diagram. So the A_n group is represented by [3ⁿ⁻¹], to imply n nodes connected by n−1 order-3 branches. Example A₂ = [3,3] = [3²] or [3^1,1] represents diagrams or .

Coxeter initially represented bifurcating diagrams with vertical positioning of numbers, but later abbreviated with an exponent notation, like [...,3^p,q] or [3^p,q,r], starting with [3^1,1,1] or [3,3^1,1] = or as D₄. Coxeter allowed for zeros as special cases to fit the A_n family, like A₃ = [3,3,3,3] = [3^4,0,0] = [3^4,0] = [3^3,1] = [3^2,2], like = = .

Coxeter groups formed by cyclic diagrams are represented by parentheseses inside of brackets, like [(p,q,r)] = for the triangle group (p q r). If the branch orders are equal, they can be grouped as an exponent as the length the cycle in brackets, like [(3,3,3,3)] = [3^[4]], representing Coxeter diagram or . can be represented as [3,(3,3,3)] or [3,3^[3]].

More complicated looping diagrams can also be expressed with care. The paracompact Coxeter group can be represented by Coxeter notation [(3,3,(3),3,3)], with nested/overlapping parentheses showing two adjacent [(3,3,3)] loops, and is also represented more compactly as [3^[ ]×[ ]], representing the rhombic symmetry of the Coxeter diagram. The paracompact complete graph diagram or , is represented as [3^[3,3]] with the superscript [3,3] as the symmetry of its regular tetrahedron coxeter diagram.

Finite groups Rank Group symbol Bracket notation Coxeter diagram 2 A2 [3] 2 B2 [4] 2 H2 [5] 2 G2 [6] 2 I2(p) [p] 3 Ih, H3 [5,3] 3 Td, A3 [3,3] 3 Oh, B3 [4,3] 4 A4 [3,3,3] 4 B4 [4,3,3] 4 D4 [31,1,1] 4 F4 [3,4,3] 4 H4 [5,3,3] n An [3n−1] .. n Bn [4,3n−2] ... n Dn [3n−3,1,1] ... 6 E6 [32,2,1] 7 E7 [33,2,1] 8 E8 [34,2,1]

Affine groups Group symbol Bracket notation Coxeter diagram ${\displaystyle {\tilde {I}}_{1},{\tilde {A}}_{1}}$ [∞] ${\displaystyle {\tilde {A}}_{2}}$ [3[3]] ${\displaystyle {\tilde {C}}_{2}}$ [4,4] ${\displaystyle {\tilde {G}}_{2}}$ [6,3] ${\displaystyle {\tilde {A}}_{3}}$ [3[4]] ${\displaystyle {\tilde {B}}_{3}}$ [4,31,1] ${\displaystyle {\tilde {C}}_{3}}$ [4,3,4] ${\displaystyle {\tilde {A}}_{4}}$ [3[5]] ${\displaystyle {\tilde {B}}_{4}}$ [4,3,31,1] ${\displaystyle {\tilde {C}}_{4}}$ [4,3,3,4] ${\displaystyle {\tilde {D}}_{4}}$ [ 31,1,1,1] ${\displaystyle {\tilde {F}}_{4}}$ [3,4,3,3] ${\displaystyle {\tilde {A}}_{n}}$ [3[n+1]] ... or ... ${\displaystyle {\tilde {B}}_{n}}$ [4,3n−3,31,1] ... ${\displaystyle {\tilde {C}}_{n}}$ [4,3n−2,4] ... ${\displaystyle {\tilde {D}}_{n}}$ [ 31,1,3n−4,31,1] ... ${\displaystyle {\tilde {E}}_{6}}$ [32,2,2] ${\displaystyle {\tilde {E}}_{7}}$ [33,3,1] ${\displaystyle {\tilde {E}}_{8}=E_{9}}$ [35,2,1]

Hyperbolic groups Group symbol Bracket notation Coxeter diagram [p,q] with 2(p + q) < pq [(p,q,r)] with ${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}<1}$ ${\displaystyle {\overline {BH}}_{3}}$ [4,3,5] ${\displaystyle {\overline {K}}_{3}}$ [5,3,5] ${\displaystyle {\overline {J}}_{3},{\tilde {H}}_{3}}$ [3,5,3] ${\displaystyle {\overline {DH}}_{3}}$ [5,31,1] ${\displaystyle {\widehat {AB}}_{3}}$ [(3,3,3,4)]   ${\displaystyle {\widehat {AH}}_{3}}$ [(3,3,3,5)]   ${\displaystyle {\widehat {BB}}_{3}}$ [(3,4,3,4)] ${\displaystyle {\widehat {BH}}_{3}}$ [(3,4,3,5)] ${\displaystyle {\widehat {HH}}_{3}}$ [(3,5,3,5)] ${\displaystyle {\overline {H}}_{4},{\tilde {H}}_{4},H_{5}}$ [3,3,3,5] ${\displaystyle {\overline {BH}}_{4}}$ [4,3,3,5] ${\displaystyle {\overline {K}}_{4}}$ [5,3,3,5] ${\displaystyle {\overline {DH}}_{4}}$ [5,3,31,1] ${\displaystyle {\widehat {AF}}_{4}}$ [(3,3,3,3,4)]

For the affine and hyperbolic groups, the subscript is one less than the number of nodes in each case, since each of these groups was obtained by adding a node to a finite group's diagram.

The Coxeter diagram usually leaves order-2 branches undrawn, but the bracket notation includes an explicit 2 to connect the subgraphs. So the Coxeter diagram = A₂×A₂ = 2A₂ can be represented by [3]×[3] = [3]² = [3,2,3]. Sometimes explicit 2-branches may be included either with a 2 label, or with a line with a gap: or , as an identical presentation as [3,2,3].

Coxeter point group rank is equal to the number of nodes which is also equal to the dimension. A single mirror exists in 1-dimension, [ ], , while in 2-dimensions [1], or [ ]×[ ]⁺. The 1 is a place-holder, not an actual branch order, but a marker for an orthogonal inactive mirror. The notation [n,1], represents a rank 3 group, as [n]×[ ]⁺ or . Similarly, [1,1] as [ ]×[ ]⁺×[ ]⁺ or order 2 and [1,1]⁺ as [ ]⁺×[ ]⁺×[ ]⁺ or , order 1!

Coxeter's notation represents rotational/translational symmetry by adding a ⁺ superscript operator outside the brackets, [X]⁺ which cuts the order of the group [X] in half, thus an index 2 subgroup. This operator implies an even number of operators must be applied, replacing reflections with rotations (or translations). When applied to a Coxeter group, this is called a direct subgroup because what remains are only direct isometries without reflective symmetry.

The ⁺ operators can also be applied inside of the brackets, like [X,Y⁺] or [X,(Y,Z)⁺], and creates "semidirect" subgroups that may include both reflective and nonreflective generators. Semidirect subgroups can only apply to Coxeter group subgroups that have even order branches adjacent to it. Elements by parentheses inside of a Coxeter group can be give a ⁺ superscript operator, having the effect of dividing adjacent ordered branches into half order, thus is usually only applied with even numbers. For example, [4,3⁺] and [4,(3,3)⁺] ().

If applied with adjacent odd branch, it doesn't create a subgroup of index 2, but instead creates overlapping fundamental domains, like [5,1⁺] = [5/2], which can define doubly wrapped polygons like a pentagram, {5/2}, and [5,3⁺] relates to Schwarz triangle [5/2,3], density 2.

Examples on Rank 2 groups

Group		Order	Generators	Subgroup		Order	Generators	Notes
[p]		2p	{0,1}	[p]+		p	{01}	Direct subgroup
[2p+] = [2p]+		2p	{01}	[2p+]+ = [2p]+2 = [p]+		p	{0101}
[2p]		4p	{0,1}	[1+,2p] = [p]	= =	2p	{101,1}	Half subgroups
				[2p,1+] = [p]	= =		{0,010}
				[1+,2p,1+] = [2p]+2 = [p]+	= =	p	{0101}	Quarter group

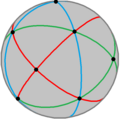
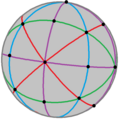
Groups without neighboring ⁺ elements can be seen in ringed nodes Coxeter-Dynkin diagram for uniform polytopes and honeycomb are related to hole nodes around the ⁺ elements, empty circles with the alternated nodes removed. So the snub cube, has symmetry [4,3]⁺ (), and the snub tetrahedron, has symmetry [4,3⁺] (), and a demicube, h{4,3} = {3,3} ( or = ) has symmetry [1⁺,4,3] = [3,3] ( or = = ).

Note: Pyritohedral symmetry can be written as , separating the graph with gaps for clarity, with the generators {0,1,2} from the Coxeter group , producing pyritohedral generators {0,12}, a reflection and 3-fold rotation. And chiral tetrahedral symmetry can be written as or , [1⁺,4,3⁺] = [3,3]⁺, with generators {12,0120}.

Example halving operations

[1,4,1] = [4]	= = [1+,4,1]=[2]=[ ]×[ ]
= = [1,4,1+]=[2]=[ ]×[ ]	= = = [1+,4,1+] = [2]+

Johnson extends the ⁺ operator to work with a placeholder 1⁺ nodes, which removes mirrors, doubling the size of the fundamental domain and cuts the group order in half.^[1] In general this operation only applies to individual mirrors bounded by even-order branches. The 1 represents a mirror so [2p] can be seen as [2p,1], [1,2p], or [1,2p,1], like diagram or , with 2 mirrors related by an order-2p dihedral angle. The effect of a mirror removal is to duplicate connecting nodes, which can be seen in the Coxeter diagrams: = , or in bracket notation:[1⁺,2p, 1] = [1,p,1] = [p].

Each of these mirrors can be removed so h[2p] = [1⁺,2p,1] = [1,2p,1⁺] = [p], a reflective subgroup index 2. This can be shown in a Coxeter diagram by adding a ⁺ symbol above the node: = = .

If both mirrors are removed, a quarter subgroup is generated, with the branch order becoming a gyration point of half the order:

q[2p] = [1⁺,2p,1⁺] = [p]⁺, a rotational subgroup of index 4. = = = = .

For example, (with p=2): [4,1⁺] = [1⁺,4] = [2] = [ ]×[ ], order 4. [1⁺,4,1⁺] = [2]⁺, order 2.

The opposite to halving is doubling^[2] which adds a mirror, bisecting a fundamental domain, and doubling the group order.

[[p]] = [2p]

Halving operations apply for higher rank groups, like tetrahedral symmetry is a half group of octahedral group: h[4,3] = [1⁺,4,3] = [3,3], removing half the mirrors at the 4-branch. The effect of a mirror removal is to duplicate all connecting nodes, which can be seen in the Coxeter diagrams: = , h[2p,3] = [1⁺,2p,3] = [(p,3,3)].

If nodes are indexed, half subgroups can be labeled with new mirrors as composites. Like , generators {0,1} has subgroup = , generators {1,010}, where mirror 0 is removed, and replaced by a copy of mirror 1 reflected across mirror 0. Also given , generators {0,1,2}, it has half group = , generators {1,2,010}.

Doubling by adding a mirror also applies in reversing the halving operation: [[3,3]] = [4,3], or more generally [[(q,q,p)]] = [2p,q].

Tetrahedral symmetry	Octahedral symmetry
Td, [3,3] = [1+,4,3] = = (Order 24)	Oh, [4,3] = [[3,3]] (Order 48)

Johnson also added an asterisk or star * operator for "radical" subgroups,^[3] that acts similar to the ⁺ operator, but removes rotational symmetry. The index of the radical subgroup is the order of the removed element. For example, [4,3*] ≅ [2,2]. The removed [3] subgroup is order 6 so [2,2] is an index 6 subgroup of [4,3].

The radical subgroups represent the inverse operation to an extended symmetry operation. For example, [4,3*] ≅ [2,2], and in reverse [2,2] can be extended as [3[2,2]] ≅ [4,3]. The subgroups can be expressed as a Coxeter diagram: or ≅ . The removed node (mirror) causes adjacent mirror virtual mirrors to become real mirrors.

If [4,3] has generators {0,1,2}, [4,3⁺], index 2, has generators {0,12}; [1⁺,4,3] ≅ [3,3], index 2 has generators {010,1,2}; while radical subgroup [4,3*] ≅ [2,2], index 6, has generators {01210, 2, (012)³}; and finally [1⁺,4,3*], index 12 has generators {0(12)²0, (012)²01}.

A trionic subgroup is an index 3 subgroup. Johnson defines a trionic subgroup with operator ⅄, index 3. For rank 2 Coxeter groups, [3], the trionic subgroup, [3^⅄] is [ ], a single mirror. And for [3p], the trionic subgroup is [3p]^⅄ ≅ [p]. Given , with generators {0,1}, has 3 trionic subgroups. They can be differentiated by putting the ⅄ symbol next to the mirror generator to be removed, or on a branch for both: [3p,1^⅄] = = , = , and [3p^⅄] = = with generators {0,10101}, {01010,1}, or {101,010}.

Trionic subgroups of tetrahedral symmetry: [3,3]^⅄ ≅ [2⁺,4], relating the symmetry of the regular tetrahedron and tetragonal disphenoid.

For rank 3 Coxeter groups, [p,3], there is a trionic subgroup [p,3^⅄] ≅ [p/2,p], or = . For example, the finite group [4,3^⅄] ≅ [2,4], and Euclidean group [6,3^⅄] ≅ [3,6], and hyperbolic group [8,3^⅄] ≅ [4,8].

An odd-order adjacent branch, p, will not lower the group order, but create overlapping fundamental domains. The group order stays the same, while the density increases. For example, the icosahedral symmetry, [5,3], of the regular polyhedra icosahedron becomes [5/2,5], the symmetry of 2 regular star polyhedra. It also relates the hyperbolic tilings {p,3}, and star hyperbolic tilings {p/2,p}

For rank 4, [q,2p,3^⅄] = [2p,((p,q,q))], = .

For example, [3,4,3^⅄] = [4,3,3], or = , generators {0,1,2,3} in [3,4,3] with the trionic subgroup [4,3,3] generators {0,1,2,32123}. For hyperbolic groups, [3,6,3^⅄] = [6,3^[3]], and [4,4,3^⅄] = [4,4,4].

Johnson identified two specific trionic subgroups^[4] of [3,3], first an index 3 subgroup [3,3]^⅄ ≅ [2⁺,4], with [3,3] ( = = ) generators {0,1,2}. It can also be written as [(3,3,2^⅄)] () as a reminder of its generators {02,1}. This symmetry reduction is the relationship between the regular tetrahedron and the tetragonal disphenoid, represent a stretching of a tetrahedron perpendicular to two opposite edges.

Secondly he identifies a related index 6 subgroup [3,3]^Δ or [(3,3,2^⅄)]⁺ (), index 3 from [3,3]⁺ ≅ [2,2]⁺, with generators {02,1021}, from [3,3] and its generators {0,1,2}.

These subgroups also apply within larger Coxeter groups with [3,3] subgroup with neighboring branches all even order.

For example, [(3,3)⁺,4], [(3,3)^⅄,4], and [(3,3)^Δ,4] are subgroups of [3,3,4], index 2, 3 and 6 respectively. The generators of [(3,3)^⅄,4] ≅ [[4,2,4]] ≅ [8,2⁺,8], order 128, are {02,1,3} from [3,3,4] generators {0,1,2,3}. And [(3,3)^Δ,4] ≅ [[4,2⁺,4]], order 64, has generators {02,1021,3}. As well, [3^⅄,4,3^⅄] ≅ [(3,3)^⅄,4].

Also related [3^1,1,1] = [3,3,4,1⁺] has trionic subgroups: [3^1,1,1]^⅄ = [(3,3)^⅄,4,1⁺], order 64, and 1=[3^1,1,1]^Δ = [(3,3)^Δ,4,1⁺] ≅ [[4,2⁺,4]]⁺, order 32.

A central inversion, order 2, is operationally differently by dimension. The group [ ]ⁿ = [2ⁿ⁻¹] represents n orthogonal mirrors in n-dimensional space, or an n-flat subspace of a higher dimensional space. The mirrors of the group [2ⁿ⁻¹] are numbered ⁠${\displaystyle 0\dots n-1}$⁠. The order of the mirrors doesn't matter in the case of an inversion. The matrix of a central inversion is ⁠${\displaystyle -I}$⁠, the Identity matrix with negative one on the diagonal.

From that basis, the central inversion has a generator as the product of all the orthogonal mirrors. In Coxeter notation this inversion group is expressed by adding an alternation ⁺ to each 2 branch. The alternation symmetry is