Hosohedron
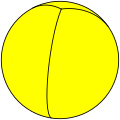
 In spherical geometry, an n-gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices. A regular n-gonal hosohedron has Schläfli symbol {2,n}, with each spherical lune having internal angle 2π/nradians (360/n degrees).[1][2] Hosohedra as regular polyhedraFor a regular polyhedron whose Schläfli symbol is {m, n}, the number of polygonal faces is : The Platonic solids known to antiquity are the only integer solutions for m ≥ 3 and n ≥ 3. The restriction m ≥ 3 enforces that the polygonal faces must have at least three sides. When considering polyhedra as a spherical tiling, this restriction may be relaxed, since digons (2-gons) can be represented as spherical lunes, having non-zero area. Allowing m = 2 makes and admits a new infinite class of regular polyhedra, which are the hosohedra. On a spherical surface, the polyhedron {2, n} is represented as n abutting lunes, with interior angles of 2π/n. All these spherical lunes share two common vertices.
Kaleidoscopic symmetryThe digonal spherical lune faces of a -hosohedron, , represent the fundamental domains of dihedral symmetry in three dimensions: the cyclic symmetry , , , order . The reflection domains can be shown by alternately colored lunes as mirror images. Bisecting each lune into two spherical triangles creates an -gonal bipyramid, which represents the dihedral symmetry , order .
Relationship with the Steinmetz solidThe tetragonal hosohedron is topologically equivalent to the bicylinder Steinmetz solid, the intersection of two cylinders at right-angles.[3] Derivative polyhedraThe dual of the n-gonal hosohedron {2, n} is the n-gonal dihedron, {n, 2}. The polyhedron {2,2} is self-dual, and is both a hosohedron and a dihedron. A hosohedron may be modified in the same manner as the other polyhedra to produce a truncated variation. The truncated n-gonal hosohedron is the n-gonal prism. Apeirogonal hosohedronIn the limit, the hosohedron becomes an apeirogonal hosohedron as a 2-dimensional tessellation: HosotopesMultidimensional analogues in general are called hosotopes. A regular hosotope with Schläfli symbol {2,p,...,q} has two vertices, each with a vertex figure {p,...,q}. The two-dimensional hosotope, {2}, is a digon. EtymologyThe term “hosohedron” appears to derive from the Greek ὅσος (hosos) “as many”, the idea being that a hosohedron can have “as many faces as desired”.[4] It was introduced by Vito Caravelli in the eighteenth century.[5] See alsoWikimedia Commons has media related to Hosohedra. References
External links |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












![{\displaystyle [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)
















![{\displaystyle [\,\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fa4c06a6c3b5a7bee90e2c44f7530e3f2a46bf8)
![{\displaystyle [2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa32363c093f4cfd50ecba68068bcfd396ea8bff)
![{\displaystyle [3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f671027d56f9c24d65c03a4a26eb0d3b933f4f15)
![{\displaystyle [4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d865272ff436d713d5069ae3066bbe07a000a99)
![{\displaystyle [5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/958ef87021d704de46ad116821bc677e07d9a5fe)
![{\displaystyle [6]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/162951515fcb56919dffe17b119f4a0aa7e9dae6)




























