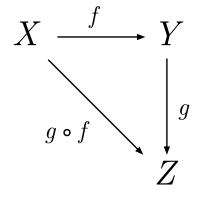范畴论

此條目需要补充更多来源。 (2022年10月9日) 请协助補充多方面可靠来源以改善这篇条目，无法查证的内容可能會因為异议提出而被移除。 致使用者：请搜索一下条目的标题（来源搜索："范畴论" — 网页、新闻、书籍、学术、图像），以检查网络上是否存在该主题的更多可靠来源（判定指引）。

範疇論（英語：Category theory）是數學的一門學科，是关于数学结构及其关系的一般理论，以抽象的方法處理數學概念，將這些概念形式化成一組組的「物件」及「態射」。數學中許多重要的領域可以形式化為範疇。使用範疇論可以令這些領域中許多難理解、難捉摸的數學結論更容易敘述證明。

一个范畴包含两类数学对象：物件与态射。以集合範疇为例，其物件為集合，態射為集合間的函數。若以第一个态射的目标为源发出第二个态射，这样形成的“复合态射”的性质同复合函数类似（存在结合律与单位态射）。但需注意，範疇的物件不一定要是集合，態射也不一定要是函數；一個數學概念若可以找到一種方法，以符合物件及態射的定義，則可形成一個有效的範疇，且所有在範疇論中導出的結論都可應用在這個數學概念之上。

範疇最簡單的例子之一為广群，其態射皆為可逆的。群胚的概念在拓撲學中很重要。範疇現在在大部分的數學分支中都有出現，在理論電腦科學的某些領域中用于對應資料型別，而在數學物理中被用來描述向量空間。

範疇論不只是對研究範疇論的人有意義，對其他數學家而言也有著其他的意思。一個可追溯至1940年代的述語「一般化的抽象廢話」，即被用來指範疇論那相對於其他傳統的數學分支更高階的抽象化。

范畴论在20世纪中叶由塞缪尔·艾伦伯格、桑德斯·麦克莱恩等人在代数拓扑工作的基础上提出。

研究範疇就是試圖以「公理化」的方法抓住在各種相關連的「數學結構」中的共同特性，並以結構間的「結構保持函數」將這些結構相關起來。因此，對範疇論系統化的研究將允許任何一個此類數學結構的普遍結論由範疇的公理中證出。

考慮下面的例子：由群組成的類Grp包含了所有具有「群結構」的物件。要證明有關群的定理，即可由此套公理進行邏輯的推導。例如，由公理中可立即證明出，群的單位元素是唯一的。

不是只專注在有特定結構的個別物件（如群）上，範疇論會著重在這些物件的態射（結構保持映射）上；經由研究這些態射，可以學到更多關於這些物件的結構。以群為例，其態射為群同態。兩個群間的群同態會嚴格地「保持群的結構」，這是個以將一個群中有關結構的訊息運到另一個群的方法，使這個群可以看做是另一個群的「過程」。因此，對群同態的研究提供了一個得以研究群的普遍特性及群公理的推論的工具。

類似的研究也出現在其他許多的數學理論中，如在拓撲學中對拓撲空間的連續映射的研究（相關範疇稱為Top），及對流形的光滑函數的研究等。

再抽象化一次，範疇自身亦為數學結構的一種，因此可以尋找在某一意義下會保持其結構的「過程」；此一過程即稱之為函子。函子將一個範疇的每個物件和另一個範疇的物件相關連起來，並將第一個範疇的每個態射和第二個範疇的態射相關連起來。

實際上，即是定義了一個「範疇和函子」的範疇，其元件為範疇，（範疇間的）態射為函子。

經由研究範疇和函子，不只是學習了一類數學結構，及在其之間的態射；還學習了「在不同類型的數學結構之間的關係」。此一基本概念首次出現於代數拓撲之中。不同的「拓撲」問題可以轉換至通常較易解答的「代數」問題之上。在拓撲空間上如基本群或基本群胚等基本的架構，可以表示成由群胚所組成的範疇之間的基本函子，而這個概念在代數及其應用之中是很普遍的。

再抽象化一次，架構通常會「自然地相關連」，這個第一眼會覺得很曖昧的概念，產生了自然變換（將一個函子映射至另一函子的方法）此一清楚的概念。許多數學上的重要架構可以從此一角度來研究。

范畴、函子和自然变换是由塞缪尔·艾伦伯格和桑德斯·麦克兰恩在1945年引进的。这些概念最初出现在拓扑学，尤其是代数拓扑学里，在同态（具有几何直观）转化成同调论（公理化方法）的过程中起了重要作用。乌拉姆说，在1930年代的后期，波兰学派中曾出现类似的想法。

艾伦堡和麦克兰说，他们的目的在于理解自然映射；为此，必须定义函子；为了定义函子，就自然地要引进范畴。

同调代数由于计算上的需要而使用范畴论，这对范畴论起到了推进作用；此后范畴论又在代数几何的公理化过程中得到发展。代数几何与罗素-怀特海德的关于数学统一性基础的观点相抵触。广义范畴论随后产生，且更容纳了语意灵活性和高阶逻辑等多种新特征的泛代数，现在被运用到数学的所有分支。

特殊范畴拓扑斯甚至可以代替公理集合论作为数学的基础。然而范畴论对这些范围广泛的基础应用还是有争议的；但作为构造性数学的基础或注释，范畴论被研究的相当透彻。尽管如此，公理集合论至今仍然是数学家们的通用语言，并没有被范畴论的注释所取代。将范畴论引入大学程度的教学（在《伯克霍夫-麦克兰》和《麦克兰-伯克霍夫》这两本抽象代数的教科书的区别上可以印证）还是遭到了相当的反对。

范畴逻辑是直觉逻辑中类型论的一个被明确定义的分支，在计算机学科的函数式编程和域理论中均有应用，并且都是在笛卡尔闭范畴中对λ演算的非句法性描述。至少，用范畴论可以精确地描述在这些相关的领域里什么是共同的（在抽象的意义上）。

一个“范畴” ${\displaystyle C}$ 由如下3個数学对象組成：

1. 一個類 ${\displaystyle \mathrm {ob} (C)}$，其元素稱為「物件」；
2. 一個類 ${\displaystyle \mathrm {hom} (C)}$，其元素稱為「態射」或「箭號」。每個態射 ${\displaystyle f}$ 都只有一個「源物件」 ${\displaystyle a}$ 及一個「目標物件」 ${\displaystyle b}$（其中 ${\displaystyle a}$ 和 ${\displaystyle b}$ 都在 ${\displaystyle \mathrm {ob} (C)}$ 內），稱之為「從 ${\displaystyle a}$ 至 ${\displaystyle b}$ 的態射」，標記為 ${\displaystyle f:a\to b}$。
   所有從 ${\displaystyle a}$ 至 ${\displaystyle b}$ 的態射所組成的類稱之為「態射類」，標記為 ${\displaystyle \mathrm {hom} (a,b)}$、 ${\displaystyle \mathrm {hom} _{C}(a,b)}$或 ${\displaystyle \mathrm {mor} (a,b)}$。
3. 一個二元運算，稱為「態射複合」，使得對任意三個物件 ${\displaystyle a}$、 ${\displaystyle b}$ 及 ${\displaystyle c}$，都會有 ${\displaystyle \circ :\mathrm {hom} (b,c)\times \mathrm {hom} (a,b)\to \mathrm {hom} (a,c)}$。兩個態射 ${\displaystyle f:a\to b}$ 及 ${\displaystyle g:b\to c}$ 的複合寫做 ${\displaystyle g\circ f}$ 或 ${\displaystyle gf}$^{[註 1]}，並會符合下列兩個公理：
   • 結合律：若 ${\displaystyle f:a\to b}$、 ${\displaystyle g:b\to c}$及 ${\displaystyle h:c\to d}$，則 ${\displaystyle h\circ (g\circ f)=(h\circ g)\circ f}$；
   • 單位元：對任意物件 ${\displaystyle x}$，總存在一個態射 ${\displaystyle 1_{x}:x\to x}$（稱為 ${\displaystyle x}$ 的單位態射），使得對每個態射 ${\displaystyle f:a\to b}$，都會有 ${\displaystyle 1_{b}\circ f=f=f\circ 1_{a}}$。

由以上公理可證得，每個物件都只存在一個單位态射。有些作者将物件本身用單位态射来定义，这在本质上是相同的。

如果对象的类确实是个集合，那么这种范畴就被称为“小范畴”。许多重要的范畴不是小范畴。

范畴中的态射有时又称为“箭號”，这种叫法来自于交换图。

每一范畴都由其对象，态射，和复合态射来表述。为了方便起见，以下的“函数”即是指态射，不再一一说明。

• Set 是所有集合和它们彼此之间的全函数构成的范畴
• Ord 是所有预序集和其间的单调函数构成的范畴
• Mag 是所有广群和其间的同态映射构成的范畴
• Med 是所有对换广群和其间的同态映射构成的范畴
• Grp 是所有群和其间的群同态构成的范畴
• Ab 是所有阿贝尔群和其间的群同态构成的范畴
• Vect_K 是所有域 ${\displaystyle K}$（${\displaystyle K}$固定）上的向量空间和其间的${\displaystyle K-}$线性映射构成的范畴
• Top 是所有拓扑空间和其间的连续函数构成的范畴
• Met 是所有度量空间和其间的测地映射构成的范畴
• Uni 是所有一致空间和其间的一致连续函数构成的范畴
• 任何偏序集${\displaystyle (P,\leq )}$构成一个小范畴，其对象是${\displaystyle P}$的元素，其态射是从${\displaystyle x}$指向${\displaystyle y}$的箭头，其中${\displaystyle x\leq y}$。
• 任何以单一对象${\displaystyle x}$（${\displaystyle x}$为任意固定集合）为基础的独异点构成一个小范畴。独异点的任意元素通过二元运算给出一个从${\displaystyle x}$到${\displaystyle x}$的映射，所有这些映射恰好是范畴的所有态射；范畴的复合态射也正好是独异点的二元运算。事实上，范畴可以看成独异点的推广；关于独异点的定义和定理有一些可以推广到范畴。
• 任何有向图对应于一个小范畴：其对象是图的顶点，其态射是图的路径，其复合态射是路径的连接。称此范畴为有向图的“自由范畴”。
• 设${\displaystyle I}$是个集合，“${\displaystyle I}$上的离散范畴”是一个小范畴，以${\displaystyle I}$的元素为对象，以${\displaystyle I}$的恒等映射为其唯一的态射。
• 任何范畴${\displaystyle C}$可以在另一种看法下成为一个新的范畴：它具有相同的对象，然而所有态射都是反方向的。称此为“对偶”或者“反范畴”，记作 ${\displaystyle C^{op}}$（${\displaystyle op}$来自英文的opposite，意為「相反」）。
• 设${\displaystyle C}$和${\displaystyle D}$是范畴，则它们的“直积范畴”${\displaystyle C\times D}$被定义为：其对象为取自${\displaystyle C}$的一个对象和取自${\displaystyle D}$的一个对象的有序对，其态射亦为取自${\displaystyle C}$的一个态射和取自${\displaystyle D}$的一个态射的有序对，其复合态射则由其分量分别复合。

映射之间的关系（比如${\displaystyle fg=h}$）在大多数情形下可用更直观的交换图来表示，在此图中对象被表示成顶点，态射被表示为箭头。

一个表为${\displaystyle f:a\rightarrow b}$的态射可具有以下任意一种性质。

• 单态射：对所有态射${\displaystyle g_{1},\ g_{2}:\ x\to a}$，若${\displaystyle f\circ g_{1}=f\circ g_{2}}$，则${\displaystyle g_{1}=g_{2}}$。
• 满态射：对所有态射${\displaystyle g_{1},\ g_{2}:\ b\to x}$，若${\displaystyle g_{1}\circ f=g_{2}\circ f}$，则${\displaystyle g_{1}=g_{2}}$
• 若${\displaystyle f}$即是单态射也是满态射，则为双态射。
• 同构：若有态射${\displaystyle g:\ b\to a}$，如${\displaystyle f\circ g=1_{b}}$和${\displaystyle g\circ f=1_{a}}$。^[a]
• 自同态：若${\displaystyle a=b}$。${\displaystyle \mathrm {end} (a)}$表示${\displaystyle a}$的自同态类。

• 自同构：若${\displaystyle f}$即同构，也自同态。${\displaystyle \mathrm {aut} (a)}$表示${\displaystyle a}$的自同构类。
• 屈态射（retraction）：若${\displaystyle f}$的右逆存在。即有态射${\displaystyle g:\ b\to a}$和${\displaystyle f\circ g=1_{b}}$。
• 切态射（section）：若${\displaystyle f}$的左逆存在。即有态射${\displaystyle g:\ b\to a}$和${\displaystyle g\circ f=1_{a}}$。

屈态射必为满态射，切态射必为单态射。另外，下面三条表述等价：

• ${\displaystyle f}$是单态射，也是屈态射；
• ${\displaystyle f}$是满态射，也是切态射；
• ${\displaystyle f}$同构。

函子是范畴之间保持结构的映射，可以看成以所有（小）范畴为成员的范畴中的态射。

一个从范畴${\displaystyle C}$到范畴${\displaystyle D}$的（协变）函子${\displaystyle F}$被定义为：

• 对${\displaystyle C}$中任意对象${\displaystyle X}$，都有一个${\displaystyle D}$中相应的对象${\displaystyle F(X)}$与其对应；
• 对${\displaystyle C}$中任意态射 ${\displaystyle f:X\rightarrow Y}$，都有一个${\displaystyle D}$中相应的态射${\displaystyle F(f):F(X)\rightarrow F(Y)}$与其对应；

并使下列性质成立：

• 对${\displaystyle C}$中任意对象${\displaystyle X}$，都有${\displaystyle F(\mathrm {id} _{x})=\mathrm {id} _{F(X)}}$。
• 对${\displaystyle C}$中任意两个态射${\displaystyle f:X\rightarrow Y}$和${\displaystyle g:Y\rightarrow Z}$，都有 ${\displaystyle F(g\cdot f)=F(g)\cdot F(f)}$。

一个从范畴${\displaystyle C}$到范畴${\displaystyle D}$的反变函子${\displaystyle F}$不同于函子的地方仅在于将${\displaystyle D}$中的映射箭头倒过来。比如说${\displaystyle f:X\rightarrow Y}$是${\displaystyle C}$中任一态射，则有${\displaystyle F(f):F(Y)\rightarrow F(X)}$。定义反变函子的最简捷的方法是作为${\displaystyle C}$的反范畴${\displaystyle C^{op}}$到${\displaystyle D}$上的函子。

有关函子的具体例子和性质请详见函子条目。

“自然变换”是两个函子之间的关系。函子通常用来描述“自然构造”，而自然变换则描述函子间的“自然同态”。有时，两个截然不同的构造会产生“相同”结果，这可以用函子之间的自然同态来表述。

如果${\displaystyle F}$和${\displaystyle G}$是从范畴${\displaystyle C}$到范畴${\displaystyle D}$的（协变）函子，则从${\displaystyle F}$到${\displaystyle G}$的一个自然变换会给${\displaystyle C}$中的每个对象${\displaystyle X}$，关联一个${\displaystyle D}$中相应的态射${\displaystyle \eta _{X}:F(X)\rightarrow G(X)}$，使得对${\displaystyle C}$中的任何态射${\displaystyle f:X\rightarrow Y}$，都有${\displaystyle \eta _{Y}\cdot F(f)=G(f)\cdot \eta _{X}}$；这也就是说下列图表是可交换的：

如有从${\displaystyle F}$到${\displaystyle G}$的自然变换，使得${\displaystyle \eta _{X}}$对${\displaystyle C}$中所有对象${\displaystyle X}$来说都同构，则称这两个函子${\displaystyle F}$和${\displaystyle G}$“自然同构”。

设${\displaystyle K}$是域，${\displaystyle V}$是${\displaystyle K}$上的任意向量空间，则有从向量空间到其二重对偶的一个“自然”內射型线性映射${\displaystyle V\rightarrow V^{**}}$ 。这些映射在以下意义上是“自然”的：二重对偶运算是一个函子，这些映射正好构成了从恒等函子到二重对偶函子的自然变换。如果向量空间的维数是有限的，我们就得到一个自然同构；因为“有限向量空间自然同构于其二重对偶”。

考虑阿贝尔群及其同态构成的范畴${\displaystyle \mathrm {Ab} }$。对任意阿贝尔群${\displaystyle X}$、${\displaystyle Y}$和${\displaystyle Z}$，我们得到群同构

${\displaystyle \mathrm {Mor} \left(X,\mathrm {Mor} \left(Y,Z\right)\right)\rightarrow \mathrm {Mor} \left(X\otimes Y,Z\right)}$ 。

这些同构是“自然”的，因为它们定义了两个函子间的一种自然变换：${\displaystyle \mathrm {Ab} ^{op}\times \mathrm {Ab} ^{op}\times \mathrm {Ab} \rightarrow \mathrm {Ab} }$。

运用范畴论的语言，许多数学研究领域都可以归结成一些恰当的范畴，例如所有集合的范畴，所有群的范畴，所有拓扑的范畴，等等。这些范畴里的确有一些“特殊的”对象，例如空集或者两个拓扑的直积。然而，在范畴的定义里，对象是原子性的，那就是说，我们无法知道一个对象到底是集合，是拓扑，还是其它抽象概念。有必要定义特殊对象而不涉及对象的内在结构，这是一个挑战。那么到底怎样不用元素而定义空集，不用开集而定义拓扑积呢？

解决这个问题的途径是借用对象和对象之间的关系，而这些关系由相应范畴中的态射给出。现在问题转化为寻找泛性质，这些泛性质可以唯一地决定我们所感兴趣的对象。事实上，为数众多的重要结构都可用纯范畴论的方法来描述。在定义泛性质时，我们要用到一个非常关键的概念：范畴性“极限”和其“上极限”。

人们很自然地要问，在什么样的情形下，两个范畴“在本质上是相同”的，换一句话来说，对其中一个范畴成立的定理，可以既定地转换成另一个范畴的定理。用来描述这种情形的主要方法是“范畴的等价性”，由函子给出。范畴的等价性在数学中有很多的应用。

范畴和函子的定义只是范畴代数中最基本的部分。除此之外的重要部分如下列所述。基本上是以阅读顺序排列，尽管它们彼此之间有着内在的联系。

• 函子范畴 ${\displaystyle D^{C}}$以从${\displaystyle C}$到${\displaystyle D}$的函子为对象，以这些函子间的自然映射为泛射。米田引理刻划了函子范畴中可表示的函子，是范畴论最著名的基本结果之一。
• 对偶原则：范畴论中，每一陈述，定理，或定义都有其“对偶”，实质上可以通过“反转所有箭头”来得到。如果一个陈述在范畴${\displaystyle C}$中成立，那么它的对偶将在其对偶范畴${\displaystyle C^{op}}$中成立。这一对偶性在范畴论的任何层次都是普适的，由于它经常不是很清晰，对偶性的应用可以揭示惊人的关联性。
• 伴随函子：两个映射方向相反的函子对称为伴随函子，随着结合的顺序不同，分别为左伴随和右伴随。通常来自于由泛性质所定义的结构；也可以作为泛性质的一种更加抽象和更加强有力的看法。

上述许多概念，特别是范畴的等价性、伴随函子和函子范畴等，可抽象至更高维的背景中。简而言之，若将态射视为“从一个对象到另一个对象的过程”，那么高维范畴就允许我们考虑“高维过程”，从而方便地概括之。

例如，（严格）2-范畴是与“态射间的态射”一起的范畴，即允许态射转换的过程。然后便可以对这些“双态射”进行横纵向的“组合”，通过规定二维的“交换律”，联系起两个合成律。这方面的标准例子是Cat，即所有（小）范畴的二维范畴，其中态射的双态射仅仅是通常意义上的态射的自然变换。另一个基本例子是，考虑一个具有单一物件的二维范畴，即幺半范畴。双范畴是比二维范畴弱的概念。其中态射的组成不是严格意义上的关联，而只是平凡的同构。

这个过程可以扩展到任意自然数维，称为n维范畴。甚至还有与序数ω对应的ω维范畴的概念。

高维范畴是更广泛的高维代数的一部分。

• 在许多范畴中，态射集合${\displaystyle \mathrm {Mor} (A,B)}$不仅仅是集合，实际上是阿贝尔群，态射的复合具有群结构，也就是说是双线性的。这种范畴被称为预加性的。如果这种范畴还具有所有有限的积和上积，则称为加性范畴。如果所有具有一个核和一个上核，那么所有满射都是上核，所有单射都是核，我们称此为阿贝尔范畴。阿贝尔范畴的一个典型的例子是阿贝尔群所组成的范畴。
• 一个范畴被称为是完备的，如果所有极限存在。集合，阿贝尔群和拓扑空间的范畴是完备的。
• 一个范畴被称为是笛卡儿闭性的，如果它具有有限直积，并且一个定义在有限乘积上的态射总是可以表示成定义在其中一个因子上的态射。
• 一个拓扑斯是一种特殊的笛卡儿闭范畴，在其中可表述（公理化）所有的数学结构（就象传统上使用集合论可以表示所有数学结构）。一个拓扑斯也可以用来表述一个逻辑理论。
• 一个群胚是这样一种范畴，其中每一个映射都是一个同构。群胚是群、群作用和等价关系的推广。

“	首先应注意到，整个范畴的概念基本上是个辅助性的概念；我们的基本概念，基本上就是函子和自然变换[...]	”
——Eilenberg和Mac Lane (1945) [1]

虽然塞缪尔·艾伦伯格和桑德斯·麦克莱恩在1942年一篇关于群论的论文中已经给出了函子和自然变换的具体例子，^[2]他们在1945年的一篇论文中，向这些概念引入了更普遍的意义，还有范畴的额外概念^[1]，并讨论了范畴论在代数拓扑领域的应用。^[3]这些工作是直观几何同调到同调代数过渡的一个重要部分。

以斯塔尼斯拉夫·乌拉姆名义写的一系列文章，都声称类似的想法在1930年代末的波兰已经流行了。艾伦伯格是波兰人，1930年代在波兰学习数学。范畴论在某种意义上也是埃米·诺特将抽象过程形式化的延续；^[4]诺特意识到，理解一种数学结构需要理解保留了结构的过程（同构）。^{[來源請求]}艾伦伯格和麦克莱恩引入了范畴，用于理解和形式化将代数结构（拓扑不变量）与拓扑学结构相关联的过程（函子）。

范畴论最初源自同调代数的需要，并为现代代数几何（概形论）的需要而得到广泛扩展。范畴论可被视为泛代数的延伸，后者研究代数结构，前者则适用于任何数学结构，并研究不同性质的结构间的关系，因此可用于整个数学领域。在数理逻辑和语义（范畴抽象机）上的应用来得较晚。

某些称作拓扑斯（topos，单数topoi）的范畴甚至可以替代公理集合论作为数学的基础。拓扑斯也可看做是特定类型的范畴，有两个额外的拓扑斯公理。范畴论的这些基础应用已经研究得相当详细，常是作为数学构成主义的基础。拓扑斯理论是抽象层论的一种形式，源于几何学，启发了诸如无点拓扑学之类想法。

范畴逻辑现在是基于直觉主义逻辑类型论，定义明确的领域，并在函数式编程和域理论中得到应用，其中一个笛卡儿闭范畴被视作λ演算的非语义描述。范畴论澄清了领域间在某种抽象意义上的共同点。

范畴论还有其他应用。例如，约翰·拜艾兹展示了物理学中费曼图和幺半范畴之间的联系。^[5]范畴论的另一个应用是拓扑斯理论，已在数学音乐理论中得到了应用，可参Guerino Mazzola的书《音乐的拓扑斯，概念、理论和表现的集合逻辑》。

1. ^ 有些作者會以不同的次序做複合，將g ∘ f 寫做fg 或f ∘ g。研究電腦科學的學者在使用範疇論時經常將 ${\displaystyle g\circ f}$ 寫做 ${\displaystyle f;g}$。

• Adámek, Jiří; Herrlich, Horst; Strecker, George E. Abstract and Concrete Categories. Heldermann Verlag Berlin. 2004 [2022-10-09]. （原始内容存档于2021-02-24）. 
• Barr, Michael; Wells, Charles, Category Theory for Computing Science, Reprints in Theory and Applications of Categories 22 3rd, 2012 [1995] [2022-10-09], （原始内容存档于2015-01-15） .
• Barr, Michael; Wells, Charles, Toposes, Triples and Theories, Reprints in Theory and Applications of Categories 12, 2005 [2022-10-09], MR 2178101, （原始内容存档于2018-02-07） .
• Borceux, Francis. Handbook of categorical algebra. Encyclopedia of Mathematics and its Applications. Cambridge University Press. 1994: 50–52. ISBN 9780521441780. 
• Freyd, Peter J. Abelian Categories. Reprints in Theory and Applications of Categories 3. 2003 [1964] [2022-10-09]. （原始内容存档于2021-02-25）. 
• Freyd, Peter J.; Scedrov, Andre. Categories, allegories. North Holland Mathematical Library 39. North Holland. 1990. ISBN 978-0-08-088701-2. 
• Goldblatt, Robert. Topoi: The Categorial Analysis of Logic. Studies in logic and the foundations of mathematics 94. Dover. 2006 [1979]. ISBN 978-0-486-45026-1. 
• Herrlich, Horst; Strecker, George E. Category Theory 3rd. Heldermann Verlag Berlin. 2007. ISBN 978-3-88538-001-6. .
• Kashiwara, Masaki; Schapira, Pierre. Categories and Sheaves. Grundlehren der Mathematischen Wissenschaften 332. Springer. 2006 [2022-10-09]. ISBN 978-3-540-27949-5. （原始内容存档于2022-10-27）. 
• Lawvere, F. William; Rosebrugh, Robert. Sets for Mathematics. Cambridge University Press. 2003. ISBN 978-0-521-01060-3.  含有內容需登入查看的頁面 (link)
• Lawvere, F. William; Schanuel, Stephen Hoel. Conceptual Mathematics: A First Introduction to Categories 2nd. Cambridge University Press. 2009 [1997]. ISBN 978-0-521-89485-2.  含有內容需登入查看的頁面 (link)
• Leinster, Tom. Higher Operads, Higher Categories. London Math. Society Lecture Note Series 298. Cambridge University Press. 2004: 448 [2006-04-03]. Bibcode:2004hohc.book.....L. ISBN 978-0-521-53215-0. （原始内容存档于2003-10-25）.  |journal=被忽略 (帮助)
• Leinster, Tom. Basic Category Theory. Cambridge Studies in Advanced Mathematics 143. Cambridge University Press. 2014 [2022-10-09]. ISBN 9781107044241. arXiv:1612.09375 . （原始内容存档于2022-10-27）. 
• Lurie, Jacob. Higher Topos Theory. Annals of Mathematics Studies 170. Princeton University Press. 2009. ISBN 978-0-691-14049-0. MR 2522659. arXiv:math.CT/0608040 . 
• Mac Lane, Saunders. Categories for the Working Mathematician. Graduate Texts in Mathematics 5 2nd. Springer-Verlag. 1998. ISBN 978-0-387-98403-2. MR 1712872. 
• Mac Lane, Saunders; Birkhoff, Garrett. Algebra 2nd. Chelsea. 1999 [1967]. ISBN 978-0-8218-1646-2. 
• Martini, A.; Ehrig, H.; Nunes, D. Elements of basic category theory. Technical Report. 1996, 96 (5) [2022-10-09]. （原始内容存档于2008-06-24）. 
• May, Peter. A Concise Course in Algebraic Topology. University of Chicago Press. 1999. ISBN 978-0-226-51183-2. 
• Mazzola, Guerino. The Topos of Music, Geometric Logic of Concepts, Theory, and Performance. Birkhäuser. 2002. ISBN 978-3-7643-5731-3. 
• Pedicchio, Maria Cristina; Tholen, Walter (编). Categorical foundations. Special topics in order, topology, algebra, and sheaf theory. Encyclopedia of Mathematics and Its Applications 97. Cambridge University Press. 2004. ISBN 978-0-521-83414-8. Zbl 1034.18001. 
• Pierce, Benjamin C. Basic Category Theory for Computer Scientists. MIT Press. 1991. ISBN 978-0-262-66071-6. 
• Schalk, A.; Simmons, H. An introduction to Category Theory in four easy movements (PDF). 2005 [2007-12-03]. （原始内容 (PDF)存档于2017-03-21）.  Notes for a course offered as part of the MSc. in Mathematical Logic, Manchester University.
• Simpson, Carlos. Homotopy theory of higher categories. 2010. Bibcode:2010arXiv1001.4071S. arXiv:1001.4071 . , draft of a book.
• Taylor, Paul. Practical Foundations of Mathematics. Cambridge Studies in Advanced Mathematics 59. Cambridge University Press. 1999. ISBN 978-0-521-63107-5. 
• Turi, Daniele. Category Theory Lecture Notes (PDF). 1996–2001 [11 December 2009]. （原始内容存档 (PDF)于2022-02-21）.  Based on Mac Lane 1998.

• "Category Theory" in Stanford Encyclopedia of Philosophy （页面存档备份，存于互联网档案馆）
• Homepage of the Categories mailing list，具有详尽的参考资料列表
• Category Theory section of Alexandre Stefanov's list of free online mathematics resources