Código binario

O código binario o/u sistema binario é un sistema de numeración posicional no que todas as cantidades se representan utilizando como base o número dous, co que se dispón de dúas cifras: cero e mais un (0 e 1).

Os computadores dixitais traballan internamente con dous niveis de voltaxe/carga, polo que o seu sistema de numeración natural é o sistema binario (aceso/ apagado). Con efecto, nun sistema simple coma este é posible simplificar o cálculo, co auxilio da lóxica booleana. En computación, chámaselle bit a un díxito binario (0 ou 1).

Ademais, este sistema de numeración permite a transmisión de datos cun risco nulo de interferencias.^{[Cómpre referencia]}

Un número binario é un número expresado no sistema numérico de base 2.^[1]

Contar é como ir sumando 1 por tanto o seguinte número dun número acabado en 0 é o mesmo acabado en 1 e se acaba en cero hai que ter en conta o carrexo e poñer a cero todos os 1 á esquerda ata o seguinte 0 que ficará a 1.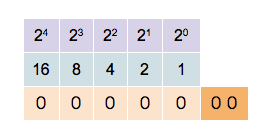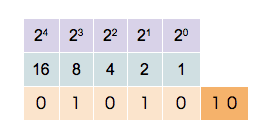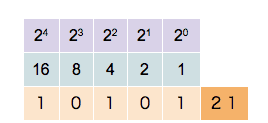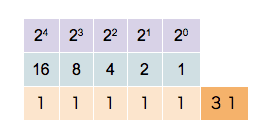

Dado un número N, binario, unha forma de convertelo en decimal é aplicar o teorema xeral da numeración posicional, e así escribir cada número que o compón (bit), multiplicado pola base do sistema (base = 2), elevado á posición que ocupa. Exemplo:

1001(binario)

1 × 2³ + 0 × 2² + 0 × 2¹ + 1 × 2⁰ = 9

Polo tanto, 1001₂ é 9 en decimal.

Dado un número decimal, para convertelo en binario, basta dividilo sucesivamente por 2, anotando o resto da división enteira:

12(decimal)

12 / 2 = 6 + 0

6 / 2 = 3 + 0

3 / 2 = 1 + 1

1 / 2 = 0 + 1

Observe que é só ler os números de baixo para riba, ou sexa 1100 é 12 en binario

Recordando as seguintes sumas básicas:

1. 0+0=0
2. 0+1=1
3. 1+1=10

Así, ao se sumar 100110101 con 11010101, tense:

      100110101
    +  11010101
    -----------
     1000001010

Opérase como en decimal: comezase a sumar desde a esquerda, no exemplo, 1+1=10, entón escríbese 0 e "levase" 1. Somase este 1 á columna seguinte: 1+0+0=1, e séguese ata terminar todas as columnas (exactamente como en decimal).

No sistema numeral orixinal, faise exactamente igual que en decimal:

      100110101
    -  11010101
    -----------
        1100000

Nas computadores, faise un método especial de suma por complemento a dous.

O produto de números binarios é especialmente simple, xa que o 0 multiplicado por calquera cousa resulta 0, e o 1 é o elemento neutro do produto.

Por exemplo, a multiplicación de 10110 por 1001:

       10110
   ×    1001
   ---------
       10110
      00000
     00000
    10110
   ---------
    11000110

Esta é unha operación un tanto complexa en binario, cuxo desenvolvemento non imos tratar.

exemplo:  21/2
          01 10/2       21   = 10101 
              0 5/2       'º        2
                1 2/2
                  0 1

• Arithmétique binaire

• Base (matemáticas).
• Número perfecto

• Probas rápidas (Matemáticas na rúa).
• conversor decimal, binario, hexadecimal.