Uncertainty principle

Part of a series of articles about
Quantum mechanics
${\displaystyle i\hbar {\frac {d}{dt}}|\Psi \rangle ={\hat {H}}|\Psi \rangle }$ Schrödinger equation
Introduction Glossary History
Background Classical mechanics Old quantum theory Bra–ket notation Hamiltonian Interference
Fundamentals Complementarity Decoherence Entanglement Energy level Measurement Nonlocality Quantum number State Superposition Symmetry Tunnelling Uncertainty Wave function Collapse
Experiments Bell's inequality CHSH inequality Davisson–Germer Double-slit Elitzur–Vaidman Franck–Hertz Leggett inequality Leggett–Garg inequality Mach–Zehnder Popper Quantum eraser Delayed-choice Schrödinger's cat Stern–Gerlach Wheeler's delayed-choice
Formulations Overview Heisenberg Interaction Matrix Phase-space Schrödinger Sum-over-histories (path integral)
Equations Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations Bayesian Consciousness causes collapse Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Many-worlds Objective-collapse Quantum logic Superdeterminism Relational Transactional
Advanced topics Relativistic quantum mechanics Quantum field theory Quantum information science Quantum computing Quantum chaos EPR paradox Density matrix Scattering theory Quantum statistical mechanics Quantum machine learning
Scientists Aharonov Bell Bethe Blackett Bloch Bohm Bohr Born Bose de Broglie Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordan Kramers Lamb Landau Laue Moseley Millikan Onnes Pauli Planck Rabi Raman Rydberg Schrödinger Simmons Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger
v t e

The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position and momentum, can be simultaneously known. In other words, the more accurately one property is measured, the less accurately the other property can be known.

More formally, the uncertainty principle is any of a variety of mathematical inequalities asserting a fundamental limit to the product of the accuracy of certain related pairs of measurements on a quantum system, such as position, x, and momentum, p.^[1] Such paired-variables are known as complementary variables or canonically conjugate variables.

First introduced in 1927 by German physicist Werner Heisenberg,^[2][3][4][5] the formal inequality relating the standard deviation of position σ_x and the standard deviation of momentum σ_p was derived by Earle Hesse Kennard^[6] later that year and by Hermann Weyl^[7] in 1928:

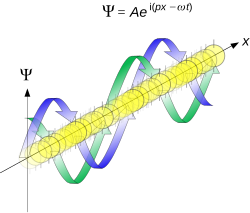
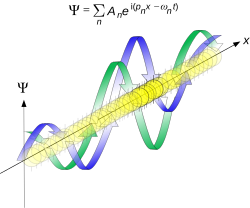
where ${\displaystyle \hbar ={\frac {h}{2\pi }}}$ is the reduced Planck constant.

The quintessentially quantum mechanical uncertainty principle comes in many forms other than position–momentum. The energy–time relationship is widely used to relate quantum state lifetime to measured energy widths but its formal derivation is fraught with confusing issues about the nature of time. The basic principle has been extended in numerous directions; it must be considered in many kinds of fundamental physical measurements.

It is vital to illustrate how the principle applies to relatively intelligible physical situations since it is indiscernible on the macroscopic^[8] scales that humans experience. Two alternative frameworks for quantum physics offer different explanations for the uncertainty principle. The wave mechanics picture of the uncertainty principle is more visually intuitive, but the more abstract matrix mechanics picture formulates it in a way that generalizes more easily.

Mathematically, in wave mechanics, the uncertainty relation between position and momentum arises because the expressions of the wavefunction in the two corresponding orthonormal bases in Hilbert space are Fourier transforms of one another (i.e., position and momentum are conjugate variables). A nonzero function and its Fourier transform cannot both be sharply localized at the same time.^[9] A similar tradeoff between the variances of Fourier conjugates arises in all systems underlain by Fourier analysis, for example in sound waves: A pure tone is a sharp spike at a single frequency, while its Fourier transform gives the shape of the sound wave in the time domain, which is a completely delocalized sine wave. In quantum mechanics, the two key points are that the position of the particle takes the form of a matter wave, and momentum is its Fourier conjugate, assured by the de Broglie relation p = ħk, where k is the wavenumber.

In matrix mechanics, the mathematical formulation of quantum mechanics, any pair of non-commuting self-adjoint operators representing observables are subject to similar uncertainty limits. An eigenstate of an observable represents the state of the wavefunction for a certain measurement value (the eigenvalue). For example, if a measurement of an observable A is performed, then the system is in a particular eigenstate Ψ of that observable. However, the particular eigenstate of the observable A need not be an eigenstate of another observable B: If so, then it does not have a unique associated measurement for it, as the system is not in an eigenstate of that observable.^[10]

The uncertainty principle can be visualized using the position- and momentum-space wavefunctions for one spinless particle with mass in one dimension.

The more localized the position-space wavefunction, the more likely the particle is to be found with the position coordinates in that region, and correspondingly the momentum-space wavefunction is less localized so the possible momentum components the particle could have are more widespread. Conversely, the more localized the momentum-space wavefunction, the more likely the particle is to be found with those values of momentum components in that region, and correspondingly the less localized the position-space wavefunction, so the position coordinates the particle could occupy are more widespread. These wavefunctions are Fourier transforms of each other: mathematically, the uncertainty principle expresses the relationship between conjugate variables in the transform.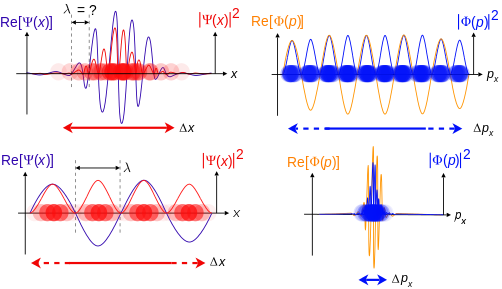

Plane wave

Wave packet

Propagation of de Broglie waves in 1d—real part of the complex amplitude is blue, imaginary part is green. The probability (shown as the colour opacity) of finding the particle at a given point x is spread out like a waveform, there is no definite position of the particle. As the amplitude increases above zero the curvature reverses sign, so the amplitude begins to decrease again, and vice versa—the result is an alternating amplitude: a wave.

According to the de Broglie hypothesis, every object in the universe is associated with a wave. Thus every object, from an elementary particle to atoms, molecules and on up to planets and beyond are subject to the uncertainty principle.

The time-independent wave function of a single-moded plane wave of wavenumber k₀ or momentum p₀ is^[11] $${\displaystyle \psi (x)\propto e^{ik_{0}x}=e^{ip_{0}x/\hbar }~.}$$

The Born rule states that this should be interpreted as a probability density amplitude function in the sense that the probability of finding the particle between a and b is $${\displaystyle \operatorname {P} [a\leq X\leq b]=\int _{a}^{b}|\psi (x)|^{2}\,\mathrm {d} x~.}$$

In the case of the single-mode plane wave, ${\displaystyle |\psi (x)|^{2}}$ is 1 if ${\displaystyle X=x}$ and 0 otherwise. In other words, the particle position is extremely uncertain in the sense that it could be essentially anywhere along the wave packet.

On the other hand, consider a wave function that is a sum of many waves, which we may write as $${\displaystyle \psi (x)\propto \sum _{n}A_{n}e^{ip_{n}x/\hbar }~,}$$ where A_n represents the relative contribution of the mode p_n to the overall total. The figures to the right show how with the addition of many plane waves, the wave packet can become more localized. We may take this a step further to the continuum limit, where the wave function is an integral over all possible modes $${\displaystyle \psi (x)={\frac {1}{\sqrt {2\pi \hbar }}}\int _{-\infty }^{\infty }\varphi (p)\cdot e^{ipx/\hbar }\,dp~,}$$ with ${\displaystyle \varphi (p)}$ representing the amplitude of these modes and is called the wave function in momentum space. In mathematical terms, we say that ${\displaystyle \varphi (p)}$ is the Fourier transform of ${\displaystyle \psi (x)}$ and that x and p are conjugate variables. Adding together all of these plane waves comes at a cost, namely the momentum has become less precise, having become a mixture of waves of many different momenta.^[12]

One way to quantify the precision of the position and momentum is the standard deviation σ. Since ${\displaystyle |\psi (x)|^{2}}$ is a probability density function for position, we calculate its standard deviation.

The precision of the position is improved, i.e. reduced σ_x, by using many plane waves, thereby weakening the precision of the momentum, i.e. increased σ_p. Another way of stating this is that σ_x and σ_p have an inverse relationship or are at least bounded from below. This is the uncertainty principle, the exact limit of which is the Kennard bound.

We are interested in the variances of position and momentum, defined as $${\displaystyle \sigma _{x}^{2}=\int _{-\infty }^{\infty }x^{2}\cdot |\psi (x)|^{2}\,dx-\left(\int _{-\infty }^{\infty }x\cdot |\psi (x)|^{2}\,dx\right)^{2}}$$ $${\displaystyle \sigma _{p}^{2}=\int _{-\infty }^{\infty }p^{2}\cdot |\varphi (p)|^{2}\,dp-\left(\int _{-\infty }^{\infty }p\cdot |\varphi (p)|^{2}\,dp\right)^{2}~.}$$

Without loss of generality, we will assume that the means vanish, which just amounts to a shift of the origin of our coordinates. (A more general proof that does not make this assumption is given below.) This gives us the simpler form $${\displaystyle \sigma _{x}^{2}=\int _{-\infty }^{\infty }x^{2}\cdot |\psi (x)|^{2}\,dx}$$ $${\displaystyle \sigma _{p}^{2}=\int _{-\infty }^{\infty }p^{2}\cdot |\varphi (p)|^{2}\,dp~.}$$

The function ${\displaystyle f(x)=x\cdot \psi (x)}$ can be interpreted as a vector in a function space. We can define an inner product for a pair of functions u(x) and v(x) in this vector space: $${\displaystyle \langle u\mid v\rangle =\int _{-\infty }^{\infty }u^{*}(x)\cdot v(x)\,dx,}$$ where the asterisk denotes the complex conjugate.

With this inner product defined, we note that the variance for position can be written as $${\displaystyle \sigma _{x}^{2}=\int _{-\infty }^{\infty }|f(x)|^{2}\,dx=\langle f\mid f\rangle ~.}$$

We can repeat this for momentum by interpreting the function ${\displaystyle {\tilde {g}}(p)=p\cdot \varphi (p)}$ as a vector, but we can also take advantage of the fact that ${\displaystyle \psi (x)}$ and ${\displaystyle \varphi (p)}$ are Fourier transforms of each other. We evaluate the inverse Fourier transform through integration by parts: $${\displaystyle {\begin{aligned}g(x)&={\frac {1}{\sqrt {2\pi \hbar }}}\cdot \int _{-\infty }^{\infty }{\tilde {g}}(p)\cdot e^{ipx/\hbar }\,dp\\&={\frac {1}{\sqrt {2\pi \hbar }}}\int _{-\infty }^{\infty }p\cdot \varphi (p)\cdot e^{ipx/\hbar }\,dp\\&={\frac {1}{2\pi \hbar }}\int _{-\infty }^{\infty }\left[p\cdot \int _{-\infty }^{\infty }\psi (\chi )e^{-ip\chi /\hbar }\,d\chi \right]\cdot e^{ipx/\hbar }\,dp\\&={\frac {i}{2\pi }}\int _{-\infty }^{\infty }\left[{\cancel {\left.\psi (\chi )e^{-ip\chi /\hbar }\right|_{-\infty }^{\infty }}}-\int _{-\infty }^{\infty }{\frac {d\psi (\chi )}{d\chi }}e^{-ip\chi /\hbar }\,d\chi \right]\cdot e^{ipx/\hbar }\,dp\\&=-i\int _{-\infty }^{\infty }{\frac {d\psi (\chi )}{d\chi }}\left[{\frac {1}{2\pi }}\int _{-\infty }^{\infty }\,e^{ip(x-\chi )/\hbar }\,dp\right]\,d\chi \\&=-i\int _{-\infty }^{\infty }{\frac {d\psi (\chi )}{d\chi }}\left[\delta \left({\frac {x-\chi }{\hbar }}\right)\right]\,d\chi \\&=-i\hbar \int _{-\infty }^{\infty }{\frac {d\psi (\chi )}{d\chi }}\left[\delta \left(x-\chi \right)\right]\,d\chi \\&=-i\hbar {\frac {d\psi (x)}{dx}}\\&=\left(-i\hbar {\frac {d}{dx}}\right)\cdot \psi (x),\end{aligned}}}$$ where ${\displaystyle v={\frac {\hbar }{-ip}}e^{-ip\chi /\hbar }}$ in the integration by parts, the cancelled term vanishes because the wave function vanishes at both infinities and ${\displaystyle |e^{-ip\chi /\hbar }|=1}$, and then use the Dirac delta function which is valid because ${\displaystyle {\dfrac {d\psi (\chi )}{d\chi }}}$ does not depend on p .

The term ${\textstyle -i\hbar {\frac {d}{dx}}}$ is called the momentum operator in position space. Applying Plancherel's theorem, we see that the variance for momentum can be written as $${\displaystyle \sigma _{p}^{2}=\int _{-\infty }^{\infty }|{\tilde {g}}(p)|^{2}\,dp=\int _{-\infty }^{\infty }|g(x)|^{2}\,dx=\langle g\mid g\rangle .}$$

The Cauchy–Schwarz inequality asserts that $${\displaystyle \sigma _{x}^{2}\sigma _{p}^{2}=\langle f\mid f\rangle \cdot \langle g\mid g\rangle \geq |\langle f\mid g\rangle |^{2}~.}$$

The modulus squared of any complex number z can be expressed as $${\displaystyle |z|^{2}={\Big (}{\text{Re}}(z){\Big )}^{2}+{\Big (}{\text{Im}}(z){\Big )}^{2}\geq {\Big (}{\text{Im}}(z){\Big )}^{2}=\left({\frac {z-z^{\ast }}{2i}}\right)^{2}.}$$ we let ${\displaystyle z=\langle f|g\rangle }$ and ${\displaystyle z^{*}=\langle g\mid f\rangle }$ and substitute these into the equation above to get $${\displaystyle |\langle f\mid g\rangle |^{2}\geq \left({\frac {\langle f\mid g\rangle -\langle g\mid f\rangle }{2i}}\right)^{2}~.}$$

All that remains is to evaluate these inner products.