Stereohedron

In geometry and crystallography, a stereohedron is a convex polyhedron that fills space isohedrally, meaning that the symmetries of the tiling take any copy of the stereohedron to any other copy.^[1]

Two-dimensional analogues to the stereohedra are called planigons. Higher dimensional polytopes can also be stereohedra, while they would more accurately be called stereotopes.

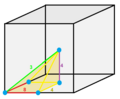
A subset of stereohedra are called plesiohedrons, defined as the Voronoi cells of a symmetric Delone set.

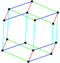
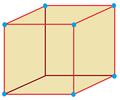
Parallelohedrons are plesiohedra which are space-filling by translation only. Edges here are colored as parallel vectors.

Parallelohedra

cube	hexagonal prism	rhombic dodecahedron	elongated dodecahedron	truncated octahedron

The catoptric tessellation contain stereohedra cells. Dihedral angles are integer divisors of 180°, and are colored by their order. The first three are the fundamental domains of ${\displaystyle {\tilde {C}}_{3}}$, ${\displaystyle {\tilde {B}}_{3}}$, and ${\displaystyle {\tilde {A}}_{3}}$ symmetry, represented by Coxeter-Dynkin diagrams: , and . ${\displaystyle {\tilde {B}}_{3}}$ is a half symmetry of ${\displaystyle {\tilde {C}}_{3}}$, and ${\displaystyle {\tilde {A}}_{3}}$ is a quarter symmetry.

Any space-filling stereohedra with symmetry elements can be dissected into smaller identical cells which are also stereohedra. The name modifiers below, half, quarter, and eighth represent such dissections.

Catoptric cells

Faces	4				5			6				8	12
Type	Tetrahedra				Square pyramid			Triangular bipyramid		Cube		Octahedron	Rhombic dodecahedron
Images	1/48 (1)	1/24 (2)	1/12 (4)	1/12 (4)	1/24 (2)	1/6 (8)	1/6 (8)	1/12 (4)	1/4 (12)	1 (48)	1/2 (24)	1/3 (16)	2 (96)
Symmetry (order)	C1 1	C1v 2	D2d 4	C1v 2	C1v 2	C4v 8	C2v 4	C2v 4	C3v 6	Oh 48	D3d 12	D4h 16	Oh 48
Honeycomb	Eighth pyramidille	Triangular pyramidille	Oblate tetrahedrille	Half pyramidille	Square quarter pyramidille	Pyramidille	Half oblate octahedrille	Quarter oblate octahedrille	Quarter cubille	Cubille	Oblate cubille	Oblate octahedrille	Dodecahedrille

Other convex polyhedra that are stereohedra but not parallelohedra nor plesiohedra include the gyrobifastigium.

Others

Faces	8		10	12
Symmetry (order)	D2d (8)			D4h (16)
Images
Cell	Gyrobifastigium	Elongated gyrobifastigium	Ten of diamonds	Elongated square bipyramid

• Ivanov, A. B. (2001) [1994], "Stereohedron", Encyclopedia of Mathematics, EMS Press
• B. N. Delone, N. N. Sandakova, Theory of stereohedra Trudy Mat. Inst. Steklov., 64 (1961) pp. 28–51 (Russian)
• Goldberg, Michael Three Infinite Families of Tetrahedral Space-Fillers Journal of Combinatorial Theory A, 16, pp. 348–354, 1974.
• Goldberg, Michael The space-filling pentahedra, Journal of Combinatorial Theory, Series A Volume 13, Issue 3, November 1972, Pages 437-443 [1] PDF
• Goldberg, Michael The Space-filling Pentahedra II, Journal of Combinatorial Theory 17 (1974), 375–378. PDF
• Goldberg, Michael On the space-filling hexahedra Geom. Dedicata, June 1977, Volume 6, Issue 1, pp 99–108 [2] PDF
• Goldberg, Michael On the space-filling heptahedra Geometriae Dedicata, June 1978, Volume 7, Issue 2, pp 175–184 [3] PDF
• Goldberg, Michael Convex Polyhedral Space-Fillers of More than Twelve Faces. Geom. Dedicata 8, 491-500, 1979.
• Goldberg, Michael On the space-filling octahedra, Geometriae Dedicata, January 1981, Volume 10, Issue 1, pp 323–335 [4] PDF
• Goldberg, Michael On the Space-filling Decahedra. Structural Topology, 1982, num. Type 10-II PDF
• Goldberg, Michael On the space-filling enneahedra Geometriae Dedicata, June 1982, Volume 12, Issue 3, pp 297–306 [5] PDF