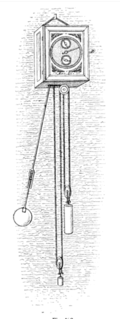
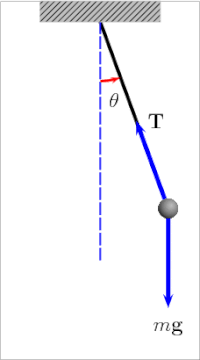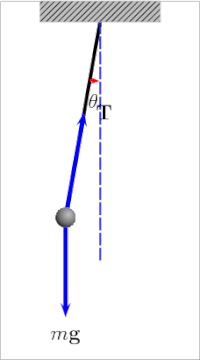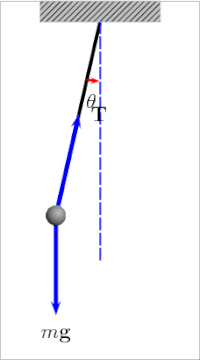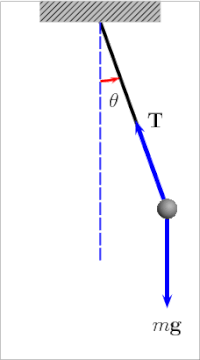
Pendulum

A pendulum is a device made of a weight suspended from a pivot so that it can swing freely.^[1] When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging back and forth. The time for one complete cycle, a left swing and a right swing, is called the period. The period depends on the length of the pendulum and also to a slight degree on the amplitude, the width of the pendulum's swing. Pendulums were widely used in early mechanical clocks for timekeeping. The SI unit of the period of a pendulum is the second (s).

The regular motion of pendulums was used for timekeeping and was the world's most accurate timekeeping technology until the 1930s.^[2] The pendulum clock invented by Christiaan Huygens in 1656 became the world's standard timekeeper, used in homes and offices for 270 years, and achieved accuracy of about one second per year before it was superseded as a time standard by the quartz clock in the 1930s. Pendulums are also used in scientific instruments such as accelerometers and seismometers. Historically they were used as gravimeters to measure the acceleration of gravity in geo-physical surveys, and even as a standard of length. The word pendulum is Neo-Latin, from the Latin pendulus, meaning 'hanging'.^[3]

The simple gravity pendulum^[4] is an idealized mathematical model of a pendulum.^[5][6][7] This is a weight (or bob) on the end of a massless cord suspended from a pivot, without friction. When given an initial push, it will swing back and forth at a constant amplitude. Real pendulums are subject to friction and air drag, so the amplitude of their swings declines.

Pendulum

Animation of a pendulum showing forces acting on the bob: the tension T in the rod and the gravitational force mg.

Animation of a pendulum showing the velocity and acceleration vectors

The period of a pendulum gets longer as the amplitude θ₀ (width of swing) increases.

The period of swing of a simple gravity pendulum depends on its length, the local strength of gravity, and to a small extent on the maximum angle that the pendulum swings away from vertical, θ₀, called the amplitude.^[8] It is independent of the mass of the bob. If the amplitude is limited to small swings,^{[Note 1]} the period T of a simple pendulum, the time taken for a complete cycle, is:^[9]

$${\displaystyle T\approx 2\pi {\sqrt {\frac {L}{g}}}\qquad \qquad \qquad \theta _{0}\ll 1{\text{ radian}}}$$

1

where ${\displaystyle L}$ is the length of the pendulum and ${\displaystyle g}$ is the local acceleration of gravity.

For small swings the period of swing is approximately the same for different size swings: that is, the period is independent of amplitude. This property, called isochronism, is the reason pendulums are so useful for timekeeping.^[10] Successive swings of the pendulum, even if changing in amplitude, take the same amount of time.

For larger amplitudes, the period increases gradually with amplitude so it is longer than given by equation (1). For example, at an amplitude of θ₀ = 0.4 radians (23°) it is 1% larger than given by (1). The period increases asymptotically (to infinity) as θ₀ approaches π radians (180°), because the value θ₀ = π is an unstable equilibrium point for the pendulum. The true period of an ideal simple gravity pendulum can be written in several different forms (see pendulum (mechanics)), one example being the infinite series:^[11][12] $${\displaystyle T=2\pi {\sqrt {\frac {L}{g}}}\left[\sum _{n=0}^{\infty }\left({\frac {\left(2n\right)!}{2^{2n}\left(n!\right)^{2}}}\right)^{2}\sin ^{2n}\left({\frac {\theta _{0}}{2}}\right)\right]=2\pi {\sqrt {\frac {L}{g}}}\left(1+{\frac {1}{16}}\theta _{0}^{2}+{\frac {11}{3072}}\theta _{0}^{4}+\cdots \right)}$$ where ${\displaystyle \theta _{0}}$ is in radians.

The difference between this true period and the period for small swings (1) above is called the circular error. In the case of a typical grandfather clock whose pendulum has a swing of 6° and thus an amplitude of 3° (0.05 radians), the difference between the true period and the small angle approximation (1) amounts to about 15 seconds per day.

For small swings the pendulum approximates a harmonic oscillator, and its motion as a function of time, t, is approximately simple harmonic motion:^[5] $${\displaystyle \theta (t)=\theta _{0}\cos \left({\frac {2\pi }{T}}\,t+\varphi \right)}$$ where ${\displaystyle \varphi }$ is a constant value, dependent on initial conditions.

For real pendulums, the period varies slightly with factors such as the buoyancy and viscous resistance of the air, the mass of the string or rod, the size and shape of the bob and how it is attached to the string, and flexibility and stretching of the string.^[11][13] In precision applications, corrections for these factors may need to be applied to eq. (1) to give the period accurately.

A damped, driven pendulum is a chaotic system.^[14][15]

Any swinging rigid body free to rotate about a fixed horizontal axis is called a compound pendulum or physical pendulum. A compound pendulum has the same period as a simple gravity pendulum of length ${\displaystyle \ell ^{\mathrm {eq} }}$, called the equivalent length or radius of oscillation, equal to the distance from the pivot to a point called the center of oscillation.^[16] This point is located under the center of mass of the pendulum, at a distance which depends on the mass distribution of the pendulum. If most of the mass is concentrated in a relatively small bob compared to the pendulum length, the center of oscillation is close to the center of mass.^[17]

The radius of oscillation or equivalent length ${\displaystyle \ell ^{\mathrm {eq} }}$ of any physical pendulum can be shown to be $${\displaystyle \ell ^{\mathrm {eq} }={\frac {I_{O}}{mr_{\mathrm {CM} }}}}$$

where ${\displaystyle I_{O}}$ is the moment of inertia of the pendulum about the pivot point ${\displaystyle O}$, ${\displaystyle m}$ is the total mass of the pendulum, and ${\displaystyle r_{\mathrm {CM} }}$ is the distance between the pivot point and the center of mass. Substituting this expression in (1) above, the period ${\displaystyle T}$ of a compound pendulum is given by $${\displaystyle T=2\pi {\sqrt {\frac {I_{O}}{mgr_{\mathrm {CM} }}}}}$$ for sufficiently small oscillations.^[18]

For example, a rigid uniform rod of length ${\displaystyle \ell }$ pivoted about one end has moment of inertia ${\textstyle I_{O}={\frac {1}{3}}m\ell ^{2}}$. The center of mass is located at the center of the rod, so ${\textstyle r_{\mathrm {CM} }={\frac {1}{2}}\ell }$ Substituting these values into the above equation gives ${\textstyle T=2\pi {\sqrt {\frac {{\frac {2}{3}}\ell }{g}}}}$. This shows that a rigid rod pendulum has the same period as a simple pendulum of two-thirds its length.

Christiaan Huygens proved in 1673 that the pivot point and the center of oscillation are interchangeable.^[19] This means if any pendulum is turned upside down and swung from a pivot located at its previous center of oscillation, it will have the same period as before and the new center of oscillation will be at the old pivot point. In 1817 Henry Kater used this idea to produce a type of reversible pendulum, now known as a Kater pendulum, for improved measurements of the acceleration due to gravity.

In physics and mathematics, in the area of dynamical systems, a double pendulum, also known as a chaotic pendulum, is a pendulum with another pendulum attached to its end, forming a simple physical system that exhibits rich dynamic behavior with a strong sensitivity to initial conditions.^[20] The motion of a double pendulum is governed by a set of coupled ordinary differential equations and is chaotic.

One of the earliest known uses of a pendulum was a 1st-century seismometer device of Han dynasty Chinese scientist Zhang Heng.^[21] Its function was to sway and activate one of a series of levers after being disturbed by the tremor of an earthquake far away.^[22] Released by a lever, a small ball would fall out of the urn-shaped device into one of eight metal toads' mouths below, at the eight points of the compass, signifying the direction the earthquake was located.^[22]

Many sources^{[23][24][25][26]} claim that the 10th-century Egyptian astronomer Ibn Yunus used a pendulum for time measurement, but this was an error that originated in 1684 with the British historian Edward Bernard.^{[27][28][29][30]}

During the Renaissance, large hand-pumped pendulums were used as sources of power for manual reciprocating machines such as saws, bellows, and pumps.^[31]

Italian scientist Galileo Galilei was the first to study the properties of pendulums, beginning around 1602.^[32] The first recorded interest in pendulums made by Galileo was around 1588 in his posthumously published notes titled On Motion,^[33][34] in which he noted that heavier objects would continue to oscillate for a greater amount of time than lighter objects. The earliest extant report of his experimental research is contained in a letter to Guido Ubaldo dal Monte, from Padua, dated November 29, 1602.^[35] His biographer and student, Vincenzo Viviani, claimed his interest had been sparked around 1582 by the swinging motion of a chandelier in Pisa Cathedral.^[36][37] Galileo discovered the crucial property that makes pendulums useful as timekeepers, called isochronism; the period of the pendulum is approximately independent of the amplitude or width of the swing.^[38] He also found that the period is independent of the mass of the bob, and proportional to the square root of the length of the pendulum. He first employed freeswinging pendulums in simple timing applications. Santorio Santori in 1602 invented a device which measured a patient's pulse by the length of a pendulum; the pulsilogium.^[39] In 1641 Galileo dictated to his son Vincenzo a design for a mechanism to keep a pendulum swinging, which has been described as the first pendulum clock;^[38] Vincenzo began construction, but had not completed it when he died in 1649.^[40]

The first pendulum clock

In 1656 the Dutch scientist Christiaan Huygens built the first pendulum clock.^[41] This was a great improvement over existing mechanical clocks; their best accuracy was improved from around 15 minutes deviation a day to around 15 seconds a day.^[42] Pendulums spread over Europe as existing clocks were retrofitted with them.^[43]

The English scientist Robert Hooke studied the conical pendulum around 1666, consisting of a pendulum that is free to swing in two dimensions, with the bob rotating in a circle or ellipse.^[44] He used the motions of this device as a model to analyze the orbital motions of the planets.^[45] Hooke suggested to Isaac Newton in 1679 that the components of orbital motion consisted of inertial motion along a tangent direction plus an attractive motion in the radial direction. This played a part in Newton's formulation of the law of universal gravitation.^[46][47] Robert Hooke was also responsible for suggesting as early as 1666 that the pendulum could be used to measure the force of gravity.^[44]

During his expedition to Cayenne, French Guiana in 1671, Jean Richer found that a pendulum clock was 2+1⁄2 minutes per day slower at Cayenne than at Paris. From this he deduced that the force of gravity was lower at Cayenne.^[48][49] In 1687, Isaac Newton in Principia Mathematica showed that this was because the Earth was not a true sphere but slightly oblate (flattened at the poles) from the effect of centrifugal force due to its rotation, causing gravity to increase with latitude.^[50] Portable pendulums began to be taken on voyages to distant lands, as precision gravimeters to measure the acceleration of gravity at different points on Earth, eventually resulting in accurate models of the shape of the Earth.^[51]

In 1673, 17 years after he invented the pendulum clock, Christiaan Huygens published his theory of the pendulum, Horologium Oscillatorium sive de motu pendulorum.^[52][53] Marin Mersenne and René Descartes had discovered around 1636 that the pendulum was not quite isochronous; its period increased somewhat with its amplitude.^[54] Huygens analyzed this problem by determining what curve an object must follow to descend by gravity to the same point in the same time interval, regardless of starting point; the so-called tautochrone curve. By a complicated method that was an early use of calculus, he showed this curve was a cycloid, rather than the circular arc of a pendulum,^[55] confirming that the pendulum was not isochronous and Galileo's observation of isochronism was accurate only for small swings.^[56] Huygens also solved the problem of how to calculate the period of an arbitrarily shaped pendulum (called a compound pendulum), discovering the center of oscillation, and its interchangeability with the pivot point.^[57]

The existing clock movement, the verge escapement, made pendulums swing in very wide arcs of about 100°.^[58] Huygens showed this was a source of inaccuracy, causing the period to vary with amplitude changes caused by small unavoidable variations in the clock's drive force.^[59] To make its period isochronous, Huygens mounted cycloidal-shaped metal guides next to the pivots in his clocks, that constrained the suspension cord and forced the pendulum to follow a cycloid arc (see cycloidal pendulum).^[60] This solution didn't prove as practical as simply limiting the pendulum's swing to small angles of a few degrees. The realization that only small swings were isochronous motivated the development of the anchor escapement around 1670, which reduced the pendulum swing in clocks to 4°–6°.^[58][61] This became the standard escapement used in pendulum clocks.

During the 18th and 19th century, the pendulum clock's role as the most accurate timekeeper motivated much practical research into improving pendulums. It was found that a major source of error was that the pendulum rod expanded and contracted with changes in ambient temperature, changing the period of swing.^[8][62] This was solved with the invention of temperature compensated pendulums, the mercury pendulum in 1721^[63] and the gridiron pendulum in 1726, reducing errors in precision pendulum clocks to a few seconds per week.^[60]

The accuracy of gravity measurements made with pendulums was limited by the difficulty of finding the location of their center of oscillation. Huygens had discovered in 1673 that a pendulum has the same period when hung from its center of oscillation as when hung from its pivot,^[19] and the distance between the two points was equal to the length of a simple gravity pendulum of the same period.^[16] In 1818 British Captain Henry Kater invented the reversible Kater's pendulum^[64] which used this principle, making possible very accurate measurements of gravity. For the next century the reversible pendulum was the standard method of measuring absolute gravitational acceleration.

In 1851, Jean Bernard Léon Foucault showed that the plane of oscillation of a pendulum, like a gyroscope, tends to stay constant regardless of the motion of the pivot, and that this could be used to demonstrate the rotation of the Earth. He suspended a pendulum free to swing in two dimensions (later named the Foucault pendulum) from the dome of the Panthéon in Paris. The length of the cord was 67 m (220 ft). Once the pendulum was set in motion, the plane of swing was observed to precess or rotate 360° clockwise in about 32 hours.^[65] This was the first demonstration of the Earth's rotation that did not depend on celestial observations,^[66] and a "pendulum mania" broke out, as Foucault pendulums were displayed in many cities and attracted large crowds.^[67][68]

Around 1900 low-thermal-expansion materials began to be used for pendulum rods in the highest precision clocks and other instruments, first invar, a nickel steel alloy, and later fused quartz, which made temperature compensation trivial.^[69] Precision pendulums were housed in low pressure tanks, which kept the air pressure constant to prevent changes in the period due to changes in buoyancy of the pendulum due to changing atmospheric pressure.^[69] The best pendulum clocks achieved accuracy of around a second per year.^[70][71]

The timekeeping accuracy of the pendulum was exceeded by the quartz crystal oscillator, invented in 1921, and quartz clocks, invented in 1927, replaced pendulum clocks as the world's best timekeepers.^[2] Pendulum clocks were used as time standards until World War 2, although the French Time Service continued using them in their official time standard ensemble until 1954.^[72] Pendulum gravimeters were superseded by "free fall" gravimeters in the 1950s,^[73] but pendulum instruments continued to be used into the 1970s.

For 300 years, from its discovery around 1582 until development of the quartz clock in the 1930s, the pendulum was the world's standard for accurate timekeeping.^[2][74] In addition to clock pendulums, freeswinging seconds pendulums were widely used as precision timers in scientific experiments in the 17th and 18th centuries. Pendulums require great mechanical stability: a length change of only 0.02%, 0.2 mm in a grandfather clock pendulum, will cause an error of a minute per week.^[75]

Clock pendulums

Longcase clock (Grandfather clock) pendulum

Ornamented pendulum in a French Comtoise clock

Mercury pendulum

Gridiron pendulum

Ellicott pendulum, another temperature compensated type

Invar pendulum in low pressure tank in Riefler regulator clock, used as the US time standard from 1909 to 1929

Pendulum and anchor escapement from a grandfather clock

Animation of anchor escapement, one of the most widely used escapements in pendulum clocks

Pendulums in clocks (see example at right) are usually made of a weight or bob (b) suspended by a rod of wood or metal (a).^[8][76] To reduce air resistance (which accounts for most of the energy loss in precision clocks)^[77] the bob is traditionally a smooth disk with a lens-shaped cross section, although in antique clocks it often had carvings or decorations specific to the type of clock. In quality clocks the bob is made as heavy as the suspension can support and the movement can drive, since this improves the regulation of the clock (see Accuracy below). A common weight for seconds pendulum bobs is 15 pounds (6.8 kg).^[78] Instead of hanging from a pivot, clock pendulums are usually supported by a short straight spring (d) of flexible metal ribbon. This avoids the friction and 'play' caused by a pivot, and the slight bending force of the spring merely adds to the pendulum's restoring force. The highest precision clocks have pivots of 'knife' blades resting on agate plates. The impulses to keep the pendulum swinging are provided by an arm hanging behind the pendulum called the crutch, (e), which ends in a fork, (f) whose prongs embrace the pendulum rod. The crutch is pushed back and forth by the clock's escapement, (g,h).

Each time the pendulum swings through its centre position, it releases one tooth of the escape wheel (g). The force of the clock's mainspring or a driving weight hanging from a pulley, transmitted through the clock's gear train, causes the wheel to turn, and a tooth presses against one of the pallets (h), giving the pendulum a short push. The clock's wheels, geared to the escape wheel, move forward a fixed amount with each pendulum swing, advancing the clock's hands at a steady rate.

The pendulum always has a means of adjusting the period, usually by an adjustment nut (c) under the bob which moves it up or down on the rod.^[8][79] Moving the bob up decreases the pendulum's length, causing the pendulum to swing faster and the clock to gain time. Some precision clocks have a small auxiliary adjustment weight on a threaded shaft on the bob, to allow finer adjustment. Some tower clocks and precision clocks use a tray attached near to the midpoint of the pendulum rod, to which small weights can be added or removed. This effectively shifts the centre of oscillation and allows the rate to be adjusted without stopping the clock.^[80][81]

The pendulum must be suspended from a rigid support.^[8][82] During operation, any elasticity will allow tiny imperceptible swaying motions of the support, which disturbs the clock's period, resulting in error. Pendulum clocks should be attached firmly to a sturdy wall.

The most common pendulum length in quality clocks, which is always used in grandfather clocks, is the seconds pendulum, about 1 metre (39 inches) long. In mantel clocks, half-second pendulums, 25 cm (9.8 in) long, or shorter, are used. Only a few large tower clocks use longer pendulums, the 1.5 second pendulum, 2.25 m (7.4 ft) long, or occasionally the two-second pendulum, 4 m (13 ft) ^[8][83] which is used in Big Ben.^[84]

The largest source of error in early pendulums was slight changes in length due to thermal expansion and contraction of the pendulum rod with changes in ambient temperature.^[85] This was discovered when people noticed that pendulum clocks ran slower in summer, by as much as a minute per week^[62][86] (one of the first was Godefroy Wendelin, as reported by Huygens in 1658).^[87] Thermal expansion of pendulum rods was first studied by Jean Picard in 1669.^[88][89] A pendulum with a steel rod will expand by about 11.3 parts per million (ppm) with each degree Celsius increase, causing it to lose about 0.27 seconds per day for every degree Celsius increase in temperature, or 9 seconds per day for a 33 °C (59 °F) change. Wood rods expand less, losing only about 6 seconds per day for a 33 °C (59 °F) change, which is why quality clocks often had wooden pendulum rods. The wood had to be varnished to prevent water vapor from getting in, because changes in humidity also affected the length.

The first device to compensate for this error was the mercury pendulum, invented by George Graham^[63] in 1721.^[8][86] The liquid metal mercury expands in volume with temperature. In a mercury pendulum, the pendulum's weight (bob) is a container of mercury. With a temperature rise, the pendulum rod gets longer, but the mercury also expands and its surface level rises slightly in the container, moving its centre of mass closer to the pendulum pivot. By using the correct height of mercury in the container these two effects will cancel, leaving the pendulum's centre of mass, and its period, unchanged with temperature. Its main disadvantage was that when the temperature changed, the rod would come to the new temperature quickly but the mass of mercury might take a day or two to reach the new temperature, causing the rate to deviate during that time.