Euclid's Elements

Elements

Papyrus Oxyrhynchus 29, a fragment of Euclid's Elements dated to c. 3rd-4th century CE. Found at Oxyrhynchus, the diagram accompanies Book II, Proposition 5.
Author	Euclid
Language	Ancient Greek
Subject	Euclidean geometry, number theory, incommensurability
Genre	Mathematics
Publication date	c. 300 BC
Pages	13 books

The Elements (Ancient Greek: Στοιχεῖα Stoikheîa) is a mathematical treatise written c. 300 BC by the Ancient Greek mathematician Euclid.

Elements is the oldest extant large-scale deductive treatment of mathematics. Drawing on the works of earlier mathematicians such as Hippocrates of Chios, Eudoxus of Cnidus, and Theaetetus, the Elements is a collection in 13 books of definitions, postulates, geometric constructions, and theorems with their proofs that covers plane and solid Euclidean geometry, elementary number theory, and incommensurability. These include the Pythagorean theorem, Thales' theorem, the Euclidean algorithm for greatest common divisors, Euclid's theorem that there are infinitely many prime numbers, and the construction of regular polygons and polyhedra.

Often referred to as the most successful textbook ever written, the Elements has continued to be used for introductory geometry from the time it was written up through the present day. It was translated into Arabic and Latin in the medieval period, where it exerted a great deal of influence on mathematics in the medieval Islamic world and in Western Europe, and has proven instrumental in the development of logic and modern science, where its logical rigor was not surpassed until the 19th century.

Euclid's Elements is the oldest extant large-scale deductive treatment of mathematics.^[1] Proclus (412–485 AD), a Greek mathematician who lived around seven centuries after Euclid, wrote in his commentary on the Elements: "Euclid, who put together the Elements, collecting many of Eudoxus' theorems, perfecting many of Theaetetus', and also bringing to irrefragable demonstration the things which were only somewhat loosely proved by his predecessors".^[a] Scholars believe that the Elements is largely a compilation of propositions based on books by earlier Greek mathematicians,^[2] including Eudoxus, Hippocrates of Chios,^[b] Thales, and Theaetetus, while other theorems are mentioned by Plato and Aristotle.^[3] It is difficult to differentiate the work of Euclid from that of his predecessors, especially because the Elements essentially superseded much earlier and now-lost Greek mathematics.^[4] The Elements version available today also includes "post-Euclidean" mathematics, probably added later by later editors such as the mathematician Theon of Alexandria in the 4th century.^[3] The classicist Markus Asper concludes that "apparently Euclid's achievement consists of assembling accepted mathematical knowledge into a cogent order and adding new proofs to fill in the gaps" and the historian Serafina Cuomo described it as a "reservoir of results".^[5][3] Despite this, historian Michalis Sialaros opines that its "remarkably tight structure" suggests that Euclid wrote the Elements himself rather than merely editing together the works of others.^[6]

Pythagoras (c. 570–495 BC) was probably the source for most of books I and II, Hippocrates of Chios (c. 470–410 BC, for book III, and Eudoxus of Cnidus (c. 408–355 BC) for book V, while books IV, VI, XI, and XII probably came from other Pythagorean or Athenian mathematicians.^[7] The Elements may have been based on an earlier textbook by Hippocrates of Chios, who also may have originated the use of letters to refer to figures.^[8]

Other similar works are also reported to have been written by Hippocrates of Chios, Theudius of Magnesia, and Leon, but are now lost.^[9][10]

The Elements does not exclusively discuss geometry as is sometimes believed.^[4][11] It is traditionally divided into three topics: plane geometry (books I–VI), basic number theory (books VII–X) and solid geometry (books XI–XIII)—though book V (on proportions) and X (on incommensurability) do not exactly fit this scheme.^[12][13] The heart of the text is the theorems scattered throughout.^[14] Using Aristotle's terminology, these may be generally separated into two categories: "first principles" and "second principles".^[15] The first group includes statements labeled as a "definition" (Ancient Greek: ὅρος or ὁρισμός), "postulate" (αἴτημα), or a "common notion" (κοινὴ ἔννοια).^[15][16] The postulates (that is, axioms) and common notions occur only in book I.^[4] Close study of Proclus suggests that older versions of the Elements may have followed the same distinctions but with different terminology, instead calling each definition a "hypothesis" (ύπόΘεςιζ) and the common notions "axioms" (άξιώμα).^[16] The second group consists of propositions, presented alongside mathematical proofs and diagrams.^[15] It is unknown whether Euclid intended the Elements as a textbook,^[6] despite its wide subsequent use as one.^[17] As a whole, the authorial voice remains general and impersonal.^[3]

Book I of the Elements is foundational for the entire text.^[4] It begins with a series of 20 definitions for basic geometric concepts such as lines, angles and various regular polygons.^[19] Euclid then presents 10 assumptions (see table, right), grouped into five postulates and five common notions.^[20] These assumptions are intended to provide the logical basis for every subsequent theorem, i.e. serve as an axiomatic system.^[21] The common notions exclusively concern the comparison of magnitudes, the sizes of geometric objects.^[22] In modern mathematics these magnitudes would be treated as real numbers measuring arc length, angle, or area, and compared numerically, but Euclid instead found ways of comparing the magnitude of shapes using geometric operations, without interpreting these magnitudes as numbers.^[23] While the first four postulates are relatively straightforward, the fifth is not. It is known as the parallel postulate, and the question of its independence from the other four postulates became the focus of a long line of research leading to the development of non-Euclidean geometry.^[22]

Book I also includes 48 propositions, which can be loosely divided into: basic theorems and constructions of plane geometry and triangle congruence (1–26), parallel lines (27-34), the area of triangles and parallelograms (35–45), and the Pythagorean theorem and its converse (46–48).^[22]

Proposition 5, that the base angles of an isosceles triangle are equal, became known in the Middle Ages as the pons asinorum, or bridge of asses, separating the mathematicians who could prove it from the fools who could not.^[24] Papyrus Oxyrhynchus 29, a 3rd-century CE papyrus, contains fragments of propositions 8-11 and 14-25.^[c] The last two propositions of Book I comprise the earliest surviving proof of the Pythagorean theorem, described by Sialaros as "remarkably delicate".^[15] The figure for the Pythagorean theorem has itself become well known under multiple names: the Bride's Chair, the windmill, or the peacock's tail.^[25]

The second book focuses on area, measured through quadrature, meaning the construction of a square of equal area to a given figure. It includes a geometric precursor of the law of cosines, and culminates in the quadrature of arbitrary rectangles.^[22] In the late 19th and 20th centuries, Book II was interpreted by some mathematical historians to establish a "geometric algebra", an expression of algebraic manipulation of linear and quadratic equations in terms of geometric concepts of length and area,^[26][27] centered on the quadratic case of the binomial theorem.^[22] This interpretation has been heavily debated since the 1970s;^[27] critics describe the characterization as anachronistic, since the foundations of even nascent algebra occurred many centuries later.^[15] Nevertheless, taken as statements about geometry, many of the propositions in this book are superfluous to modern mathematics, as they can be subsumed by the use of algebra.^[28]

Proposition 11 of Book II subdivides a given line segment into extreme and mean proportions, now called the golden ratio. It is the first of several propositions involving this ratio: It is later used in Book IV to construct a golden triangle and regular pentagon and in Book XIII to construct the regular dodecahedron and regular icosahedron, and studied as a ratio in Book VI Proposition 30.^[29][30]

Book III begins with a list of 11 definitions, and follows with 37 propositions that deal with circles and their properties. Proposition 1 is on finding the center of a circle. Propositions 2 through 15 concern chords, and intersecting and tangent circles. Tangent lines to circles are the subjects of propositions 16 through 19. Next are propositions on inscribed angles (20 through 22), and on chords, arcs, and angles (23 through 30), including the inscribed angle theorem relating inscribed to central angles as proposition 20. Propositions 31 through 34 concern angles in circles, including Thales's theorem that an angle inscribed in a semicircle is a right angle (part of proposition 31). The remaining propositions, 35 through 37, concern intersecting chords and tangents; proposition 35 is the intersecting chords theorem, and proposition 36 is the tangent–secant theorem.^[31]

Book IV treats four problems systematically for different polygons: inscribing a polygon within a circle, circumscribing a polygon about a circle, inscribing a circle within a polygon, and circumscribing a circle about a polygon.^[32] These problems are solved in sequence for triangles and then for constructible regular polygons (i.e., those that have a straightedge and compass construction) with 4, 5, 6, and 15 sides.^[4]

Book V, which is independent of the previous four books, concerns ratios of magnitudes (intuitively, how much bigger or smaller one shape is relative to another) and the comparison of ratios.^[33] Heath and other translators have formulated its first six propositions in symbolic algebra, as forms of the distributive law of multiplication over division and the associative law for multiplication. However, Leo Corry argues that this is anachronistic and misleading, because Euclid did not treat magnitudes as numbers, nor taking a ratio as a binary operation from numbers to numbers.^[34]

Much of Book V was probably ascertained from earlier mathematicians, perhaps Eudoxus,^[15] although certain propositions, such as V.16, dealing with "alternation" (if a : b :: c : d, then a : c :: b : d) likely predate Eudoxus.^[35]

Christopher Zeeman has argued that Book V's focus on the behavior of ratios under the addition of magnitudes, and its consequent failure to define ratios of ratios, was a flaw that prevented the Greeks from finding certain important concepts such as the cross ratio (central to projective geometry).^[36]

Book VI utilizes the theory of ratios from Book V in the context of plane geometry,^[4] especially the construction and recognition of similar figures. It is built almost entirely of its first proposition:^[37] "Triangles and parallelograms which are under the same height are to one another as their bases". That is, if two triangles have the same height, the ratio of their areas is the same as the ratio of lengths of their two base segments (and analogously for two parallelograms of the same height). This proposition provides a connection between ratios of lengths and ratios of areas.^[38] Proposition 25 constructs, from any two polygons, a third polygon similar to the first and with the same area as the second. Plutarch attributes this construction to Pythagoras, calling it "more subtle and more scientific" than the Pythagorean theorem. The famous ancient Greek problem of doubling the cube, now known impossible with compass and straightedge, is a special case of the analogous 3d problem of constructing a figure with a specified shape and volume.^[39] The book ends as it begins, by connecting two types of ratios: ratios of angles, and ratios of circular arc lengths, in proposition 33.^[40]

Number theory, the theory of the arithmetic of natural numbers, is covered by books VII to X. Book VII begins with a set of 22 definitions for parity (whether a number is even or odd), prime numbers, and other arithmetic-related concepts.^[4] The first of these definitions is for the unit (in modern terms, the number one), while the second states that "a number is a multitude composed of units";^[41] this is generally interpreted to mean that, for Euclid, one is not a number, and the natural numbers begin at two.^[42]

Book VII deals with elementary number theory, and includes 39 propositions, which can be loosely divided into: the Euclidean algorithm, a method for determining whether numbers are relatively prime and for finding the greatest common divisor (1-4), fractions (5-10), the theory of proportions for numbers (11-19), prime and relatively prime numbers and the theory of greatest common divisors, (20-32), and least common multiples (33-39).^[43]

The topic of Book VIII is geometric progressions.^[43] For Euclid, these were defined by the property of being in continued proportion (each two consecutive magnitudes have the same ratio) rather than, as in modern treatments, by exponentiation (the ${\displaystyle i}$th term of the progression has the form ${\displaystyle ax^{i}}$ for constants ${\displaystyle a}$ and ${\displaystyle x}$). This allowed Euclid to avoid multiplication of more than two values, but led to some awkward proofs of facts that exponential notation would make obvious.^[44]

The first part of Book VIII (propositions 1 through 10) deals with the construction and existence of geometric progressions of integers in general, and the divisibility of members of a geometric progression by each other. Propositions 11 to 27 deal with square numbers and cube numbers in geometric progressions, and the relation between these special progressions and the elements two or three steps apart in an arbitrary geometric progression.^[43]

After continuing the investigations of Book VIII on squares and cubes in geometric progressions,^[43] Book IX applies the results of the preceding two books and gives the infinitude of prime numbers (Euclid's theorem, proposition 20), the formula for the sum of a finite geometric series (proposition 35) and a construction using this sum for even perfect numbers (proposition 36). Here, a number is perfect if it equals the sum of its proper divisors, as for instance 28 = 1 + 2 + 4 + 7 + 14.^[4][45] Alhazen conjectured c. 1000, and in the 18th century Leonhard Euler proved, that this construction generates all even perfect numbers. This result is the Euclid–Euler theorem.^[46]

Of the Elements, book X is by far the largest and most complex, dealing with (in modern terms) irrational numbers in the context of magnitudes.^[15][47] Proposition 9 (as restated in modern terms) proves the irrationality of the square roots of all non-square integers such as ${\displaystyle {\sqrt {2}}}$, the square root of 2.^[48] A lemma to Proposition 29 gives Euclid's formula, for producing all fundamental Pythagorean triples^[49] Additionally, this book classifies irrational lengths into thirteen disjoint categories, related to their construction by various combinations of other lengths that are integers and their square roots.^[50] However, Wilbur Knorr warns that "The student who approaches Euclid's Book X in the hope that its length and obscurity conceal mathematical treasures is likely to be disappointed. ... the mathematical ideas are few."^[51]

Rather than treating magnitudes as real numbers, and asking whether these are rational numbers, Euclid handles this material in terms of the commensurability of lengths or areas: whether two line segments or two rectangles can both be measured by an integer number of copies of a common subunit.^[47] His classification of lengths as rational or irrational differs from the modern meaning: for Euclid, a line segment is rational when the square on its side has a rational area. That is, for Euclid, a length such as ${\displaystyle {\sqrt {2}}}$ that is the square root of a rational area is itself rational.^[52]

This book is connected to a short passage in Plato's dialogue Theaetetus among Socrates, Theodorus of Cyrene, and Theaetetus, a younger mathematician. This passage discusses a proof by Theodorus that the non-square integers from 3 to 17 have irrational square roots (after the much earlier discovery of the irrationality of ${\displaystyle {\sqrt {2}}}$), the generalization of this result to all non-square integers by Theaetetus, and a partial classification of the irrational numbers (with fewer than 13 classes).^[53][54]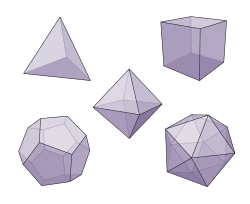

The final three books primarily discuss solid geometry.^[12] By introducing a list of 37 definitions, Book XI contextualizes the next two.^[55] Although its foundational character resembles Book I, unlike Book I it features no axiomatic system or postulates.^[55]

Book XI generalizes the results of book VI to solid figures: perpendicularity, parallelism, volumes, and similarity of parallelepipeds (polyhedra with three pairs of parallel faces). The three sections of Book XI include content on: solid geometry (1-19), solid angles (20-23), and parallelepipeds (24-37).^[55]

Book XII studies the volumes of cones, pyramids, and cylinders in detail by using the method of exhaustion, a precursor to integration,^[55] and shows, for example, that the volume of a cone is a third of the volume of the corresponding cylinder.^[56] It concludes by showing that the volume of a sphere is proportional to the cube of its radius (in modern language) by approximating its volume by a union of many pyramids.^[57]

Book XIII constructs the five Platonic solids (regular polyhedra) inscribed in a sphere, compares the ratios of their edges to the radius of the sphere,^[58] and concludes the Elements by proving that these are the only regular polyhedra.^[59]

Two additional books, that were not written by Euclid, Books XIV and XV, have been transmitted in the manuscripts of the Elements:^[60]

• Book XIV was likely written by Hypsicles, following a treatise by Apollonius of Perga. It continues the study in Book XIII of the Platonic solids and their circumscribed spheres. It concludes that, for a dodecahedron and icosahedron inscribed in a common sphere, the ratio of their surface areas and the ratio of their volumes are equal, both being^[60]$${\displaystyle {\sqrt {\frac {10}{3(5-{\sqrt {5}})}}}={\sqrt {\frac {5+{\sqrt {5}}}{6}}}.}$$
• Book XV may have been written by a student of Isidore of Miletus. It also studies the Platonic solids; it inscribes some of them within each other, counts their edges and vertices (without however finding Euler's formula ${\displaystyle V-E+F=2}$ relating these counts to each other), and computes the dihedral angles between their faces.^[60]

The practice of adding to the works of famous authors, exemplified by these books, was not unusual in ancient Greek mathematics.^[60]

Euclid's axiomatic approach and constructive methods were widely influential.^[62][63]

Many of Euclid's propositions were constructive, demonstrating the existence of some figure by detailing the steps he used to construct the object using a compass (circle-drawing tool) and straightedge (unmarked ruler). His constructive approach appears even in his geometry's postulates, as the first and third postulates stating the existence of a line and circle are constructive. Instead of stating that lines and circles exist per his prior definitions, he states that it is possible to 'construct' a line and circle. It also appears that, for him to use a figure in one of his proofs, he needs to construct it in an earlier proposition. For example, he proves the Pythagorean theorem by first inscribing a square on the sides of a right triangle, but only after constructing a square on a given line one proposition earlier.^[64]

The presentation of each result is given in a stylized form, which, although not invented by Euclid, is recognized as typically classical. It has six different parts: First is the 'enunciation', which states the result in general terms (i.e., the statement of the proposition). Then comes the 'setting-out', which gives the figure and denotes particular geometrical objects by letters. Next comes the 'definition' or 'specification', which restates the enunciation in terms of the particular figure. Then the 'construction' or 'machinery' follows. Here, the original figure is extended to forward the proof. Then, the 'proof' itself follows. Finally, the 'conclusion' connects the proof to the enunciation by stating the specific conclusions drawn in the proof, in the general terms of the enunciation.^[65]

No indication is given of the method of reasoning that led to the result, although a different book by Euclid, Data, does provide instruction about how to approach the types of problems encountered in the first four books of the Elements.^[66] For proofs involving case analysis, the Elements often includes details only of the most difficult case; some of these case analyses have been filled out by later editors such as Theon.^[67]

Euclid's presentation was limited by the mathematical ideas and notations in common currency in his era, and this causes the treatment to seem awkward to the modern reader in some places. For example, there was no notion of an angle greater than two right angles,^[68] the number 1 was sometimes treated separately from other positive integers, and, as multiplication was treated geometrically, as the area of a rectangle with given side lengths, he did not use the product of more than 3 different numbers. The geometrical treatment of number theory may have been because the alternative would have been the extremely awkward Alexandrian system of numerals,^[69] an alphabetic numeral system in which each Greek letter represented a single-digit multiple of a power of ten.^[70]

Euclid's Elements has been referred to as the most successful textbook ever written.^[17][71] The Elements is often considered after the Bible as the most frequently translated, published, and studied book in history.^[72] With Aristotle's Metaphysics, the Elements is perhaps the most successful ancient Greek text, and was the dominant mathematical textbook in the Medieval Islamic world and Western Europe.^[72][71] It was one of the very earliest mathematical works to be printed after the invention of the printing press and has been estimated to be second only to the Bible in the number of editions published since the first printing in 1482,^[73][74] the number reaching well over one thousand.^[74]

The oldest extant evidence for Euclid's Elements are a set of six ostraca (clay fragments with writing scratched onto them) found among the Elephantine papyri and ostraca, from the 3rd century BC that deal with propositions XIII.10 and XIII.16, on the construction of a dodecahedron.^[75] A papyrus recovered from Herculaneum^[76] contains an essay by the Epicurean philosopher Demetrius Lacon on Euclid's Elements.^[75] The earliest extant papyrus containing the actual text of the Elements is Papyrus Oxyrhynchus 29, a fragment containing the text of Book II, Proposition 5 and an accompanying diagram, dated to c. 75–125 AD.^[77]

Copies of the Greek text still exist, some of which can be found in the Vatican Library and the Bodleian Library in Oxford.^[d][e] The manuscripts available are of variable quality, and often incomplete.^[78] By careful analysis of the translations and originals, hypotheses have been made about the contents of the original text.^[79] Also of importance are the scholia, or annotations to the text. These additions, which often distinguished themselves from the main text (depending on the manuscript), gradually accumulated over time as opinions varied upon what was worthy of explanation or further study.^[80]

In the 4th century AD, Theon of Alexandria produced an edition of Euclid which was so widely used that it became the only surviving Greek-language source (in multiple manuscripts) until François Peyrard's 1808 discovery at the Vatican of a manuscript not derived from Theon's.^[81] This manuscript, MS. Vat.gr.190,^[d] was transcribed in the 10th century. It does not include text identifying itself as edited by Theon, and is missing a corollary to Book VI Proposition 33, claimed by Theon to be his own addition. Both Greek versions include many explanations, beyond the propositions and their proofs, that are missing from the Arabic translations of the Elements. This sparked a 19th-century academic debate between M. Klamroth and J. L. Heiberg over whether the differences between the various versions reflected abridgements or additions to Euclid's text. Revisiting this issue, Wilbur Knorr sides with Klamroth in suggesting that the Arabic sources were closer to the original, but concludes that "We have never had a 'genuine' text of Euclid, and we never will have one."^[81]

Although Euclid was known to Cicero, for instance, no record exists of the text having been translated into Latin prior to Boethius in the fifth or sixth century.^[82]

From classical antiquity until the western invention of printing, texts such as the Elements were preserved and duplicated through the process of copying manuscripts. This was laborious and expensive so manuscripts were often confined to the collections of the wealthy or to institutions such as the House of Wisdom in the medieval Islamic world or the monasteries and early universities of medieval Europe.^[83]

The Islamic world received the Elements from the Byzantine Empire around 760. According to sources from that milieu, this version was translated into Arabic under Harun al-Rashid (c. 800),^[82] in two versions by Al-Ḥajjāj ibn Yūsuf ibn Maṭar. Another Arabic translation was made later in the 9th century by Ishaq ibn Hunayn and revised by Thābit ibn Qurra.^[84][85] Although most Arabic manuscripts have been attributed to one or another of these translations, some mix material from both,^[84] and their attributions are not always in accord with the evidence from textual similarities in surviving manuscripts.^[85] This mixture was also passed down into medieval translations into Hebrew from the Arabic.^[84]

The Byzantine scholar Arethas commissioned the copying of one of the Greek manuscripts of Euclid in the late ninth century;^[86] it and another Byzantine manuscript are the two oldest surviving copies of the Greek text.^[87] Although known in Byzantium, the Elements was lost to Western Europe until about 1120,^[88][f] when the English monk Adelard of Bath translated it into Latin from an Arabic translation.^[89] A relatively recent discovery was made of a Greek-to-Latin translation from the 12th century at Palermo, Sicily. The name of the translator is not known other than he was an anonymous medical student from Salerno who was visiting Palermo in order to translate the Almagest to Latin. The Euclid manuscript is extant and quite complete.^[88]

After Adelard's translation (which became known as Adelard I), there was a flurry of translations from Arabic. Notable translators in this period include Herman of Carinthia who wrote an edition around 1140, Robert of Chester (his manuscripts are referred to collectively as Adelard II, written on or before 1251), John of Tynemouth^[90] (late 12th century; his manuscripts are referred to collectively as Adelard III), and Gerard of Cremona (sometime after 1120 but before 1187). The detailed transmission history of these translations is still an active area of research.^[91] Campanus of Novara relied heavily on these Arabic translations to create his edition (sometime before 1260) which ultimately came to dominate Latin editions until the availability of Greek manuscripts in the 16th century. There are more than 100 pre-1482 Campanus manuscripts still available today.^[92][g] After its availability in Europe, the first books of the Elements became standard in medieval universities as part of the quadrivium, the second stage of instruction after the trivium of grammar, logic, and rhetoric.^[83]

The first printed edition of the Elements appeared in 1482 (based on Campanus's translation),^[93] and since then it has been translated into many languages and published in over a thousand different editions.^[74] Theon's Greek edition was recovered and translated into Latin in an edition published in Venice in 1505 by Bartolomeo Zamberti [de].^[94] The Greek text itself was published in 1533.^[95] The first to translate the Elements into a modern European language was Nicolo Tartaglia, who published an Italian edition in 1543.^[96]

In 1570, John Dee provided a widely respected "Mathematical Preface", along with copious notes and supplementary material, to the first English edition by Henry Billingsley.^[97][98][99] In 1607, The Italian Jesuit Matteo Ricci and the Chinese mathematician Xu Guangqi published the first Chinese edition of Euclid's Elements.^[100]

The Renaissance also saw the creation of new works about polyhedra, illustrated with perspective drawings, including Piero della Francesca's De quinque corporibus regularibus (late 1400s), its plagiarism by Luca Pacioli as Divina proportione (1498, illustrated by Leonardo da Vinci), and Wenzel Jamnitzer's Perspectiva corporum regularium (1568).^[101] The Elements were the main inspiration behind della Francesca's initial work in this direction.^[102][103] Pacioli lectured in Venice on Euclid, and his commentary was included in a 1509 edition of the Elements.^[104] Jamnitzer, likewise, credits the Elements in the subtitles of his book.^[105]

Although this period also saw an explosion in newly published textbooks, teachers often stuck to the classics: a list of recommended readings by 16th century Dutch humanist Joachim Sterck van Ringelbergh, for instance, lists the Elements as its only mathematics book.^[106] Even after printed versions existed, a university might expect its students to copy by hand material from the university's copy of the Elements.^[107]

In the 19th century the Elements fell out of favor as a geometry textbook, in part supplanted by newer textbooks such as one by Adrien-Marie Legendre,^{[108][109][110]} in part because of the rise of other forms of geometry including non-Euclidean geometry, analytic geometry, and descriptive geometry,^[111][112] and in part out of pressure for an approach to mathematics education with more emphasis on intuition and less on memorization.^[111][113] Charles Dodgson (better known as Lewis Carroll), in particular, railed again this replacement of Euclid in his book Euclid and His Modern Rivals (1879).^[108] Another defender of the Elements, mathematician and historian W. W. Rouse Ball, remarked that "the fact that for two thousand years [the Elements] was the usual text-book on the subject raises a strong presumption that it is not unsuitable for that purpose."^[68] Despite falling out of wide use in education, the Elements is still occasionally used as a textbook in experimental education projects.^[114]

The Elements remains an object of scholarly study for the history of mathematics, and it has had significant influence on two areas of modern mathematics, the development of non-Euclidean geometry^[115][116] and of the axiomatic method.^[117][118]

The geometrical system established by the Elements long dominated the field; however, today that system is often referred to as 'Euclidean geometry' to distinguish it from other non-Euclidean geometries discovered in the early 19th century.^[72]

One of the most notable influences of Euclid on modern mathematics and, beyond mathematics, modern physics and the discovery of general relativity, is the discussion of the parallel postulate.^[115][116] In Book I, Euclid lists five postulates, the fifth of which stipulates

If a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.

This postulate plagued mathematicians for centuries due to its apparent complexity compared with the other four postulates. Many attempts were made to prove the fifth postulate based on the other four, but they never succeeded. Eventually in 1829, mathematician Nikolai Lobachevsky published a description of acute geometry (or hyperbolic geometry), a geometry which assumed a different form of the parallel postulate. It is in fact possible to create a valid geometry without the fifth postulate entirely, or with different versions of the fifth postulate (elliptic geometry). If one takes the fifth postulate as a given, the result is Euclidean geometry.^[119]

The axiomatic reasoning of Euclid's Elements was long considered to set the standard for mathematical rigor,^[120] but the issues of the soundness and completeness of Euclid's axioms came to the foreground in the late 19th century, when gaps were found in his reasoning^[121] and when David Hilbert began seeking "to revive Euclid’s axiomatic point of view", to develop improved axiom systems through which all mathematical and physical questions could be answered by simple calculations.^[117] Hilbert's hopes were dashed in the foundational crisis of the early 20th century, in which Kurt Gödel and others discovered that any sound axiom system for set theory must necessarily be incomplete.^[122] In the 21st century, a new standard for rigor arose, computer-assisted proofs, and the propositions of the Elements (with some updates to their proofs) have withstood computer checking.^[118][123]

Some of the foundational proofs of the Elements use assumptions that Euclid did not state explicitly as axioms. For example, in the first construction of Book 1, of an equilateral triangle, Euclid used a premise that was neither postulated nor proved: that two circles sharing the same line segment as a radius will cross each other in two points, rather than somehow not crossing.^[124][125] This example depends only on topological properties of its diagram, which remain evident even if the diagram is drawn inaccurately.^[126] However, in other cases, Euclid did not prove that certain objects were distinct or separated from each other, and the possibility that they might coincide (a type of degeneracy) might not be evident from a single diagram. An example occurs in Euclid's bisection of an angle, by constructing an isosceles triangle on the given angle and an equilateral triangle with the same base, and connecting by a line the apexes of the two triangles. This breaks down when the initial angle is 60° and the two apexes coincide.^[123]

Later editors of the Elements have included these implicit axiomatic assumptions, such as Pasch's axiom,^[127][128] in their editions' lists of formal axioms.^[129] Early attempts to construct a more complete set of axioms include Hilbert's geometry axioms^[130][131] and Tarski's.^[127][132] In 2017, Michael Beeson et al. used computer proof assistants to create and check a set of axioms similar to Euclid's. Beeson et al. chose Tarski's system as their starting point, instead of Hilbert's, because it is closer to Euclid's, and uses only points as the variables in its formulas. They provided computer-verified proofs of all propositions in Book I, using these axioms, and they also proved (using a separate logical formalization of the real numbers) that all of their axioms are valid for the points of the Cartesian coordinate system.^[123]

Over one thousand editions of Euclid's Elements have been published,^[74] in Greek, Latin, English, and other languages. Some of the more significant of these include:

• Preclarissimus liber elementorum Euclidis perspicacissimi in artem geometriam incipit quam foelicissime. Venice: Erhard Ratdolt. 1482. The editio princeps (in Latin), based on the 13th century translation and commentary of Campanus.^[133]
• Zamberti, Bartolomeo, ed. (1505). Euclidis megarẽsis philosophi platonici. Venice. First full-text Latin translation directly from the Greek.^[94] The confusion in the title between Euclid of Alexandria, the author of the Elements, and Euclid of Megara, a philosopher from almost a century earlier, was a common mistake in the Middle Ages and Renaissance.^[134]
• Lefèvre d'Étaples, Jacques, ed. (1516). Euclidis Megarensis Geometricorum elementorum liber XV. Paris: Henri Estienne. Based on Campanus and Zamberti, but without some of Zamberti's commentary. The first edition published in France.^[135]
• Grynaeus, Simon, ed. (1533). Ευκλείδου Στοιχεῖον. Basel: Johann Herwagen. Editio princeps of the Greek text. Based on two Greek manuscripts, Paris gr. 2343 and Venetus Marcianus 301,^[136] both "very inferior ones".^[94]
• Tartalea, Nicolo, ed. (1543). Euclide megarense philosopho solo introduttore delle scientie mathematice. Venice: Rossinelli. Tartaglia's translation of the Elements into Italian was the first into any modern European language, and was based on both Campanus and Zamberti. It was revised in 1565 and reprinted in 1569 and 1586.^[96]
• Magnien, Jean, ed. (1557). Euclidis Elementorum libri XV grœce et latine. Paris: Cavellat. Greek with Latin translation. Revised posthumously by Stephanus Gracilis; incorporates a translation of Book X by Pierre de Montdoré. Most proofs omitted.^[137]
• Billingsley, H., ed. (1570). The Elements of Geometrie. Preface by John Dee. London: John Daye. The first published English-language edition.^[99]
• Commandino, Federico, ed. (1572). Euclidis Elementorum Libri XV. Pisauri [Pesaro, Italy]: Apud Camillum Francischinum. In Latin. "The reference edition for the scholarly community up until the early nineteenth century"; Italian translation published in 1575 by Commandino's son-in-law, Valerio Spaccioli.^[138]
• Clavius, Christopher, ed. (1574). Euclidis elementorum libri XV. Rome: Apud Vincentium Accoltum. Latin, with added commentary by Clavius. Published in an expanded 2nd edition in 1584. Based on multiple sources, but most closely related to the version of Magnien and Gracilis.^[135]
• Nasir al-Din al-Tusi (1594). Kitāb taḥrīr uṣūl li-Uqlīdus [The Recension of Euclid's "Elements"] (in Arabic). Rome: Typographia Medicea. Based on Laurentian Library MS. Or. 20, a copy of MS. Or. 50.^[139]
• Ricci, Matteo; Xu, Guangqi, eds. (1607). Jī hé yuán běn 幾何原本 [Source of quantity] (in Chinese). Beijing. Translated from the Latin edition of Clavius, but including only books I-VI.^[100] This translation, together with a later translation of the remaining books, can be found on s:zh:幾何原本.
• Briggs, Henry, ed. (1620). Eukleidou Stoicheiōn biblia 13 / Elementorum Euclidis libri tredecim. London: William Jones. Despite the title this includes only the first six books, with parallel columns of Greek from Grynaeus 1533 and Latin corrected from Commandino 1572. The first edition in either language published in England.^[99]
• Barrow, Isaac, ed. (1659). Euclidis Elementorum [in Latin]. Euclide's Elements (1660) [in English]. Many later editions.^[99]
• Simson, Robert, ed. (1806). The elements of Euclid, viz. the first six books, together with the eleventh and twelfth. London: F. Wingrave.^[140] Revised in 1862 by Isaac Todhunter and republished in 1933 by E. P. Dutton, Everyman's Library 891.^[141]
• Byrne, Oliver (1847). The first six books of the elements of Euclid, in which coloured diagrams and symbols are used instead of letters for the greater ease of learners. London: William Pickering.^[142][143] Facsimile edited by Oechslin, Werner (2010). Taschen. ISBN 3836517752.^[143] Euclid's Elements: Completing Oliver Byrne's work, a modern redrawing extended to the rest of the Elements, was published by Kronecker Wallis, 2019.^[144]
• Casey, John, ed. (1882). The First Six Books of the Elements of Euclid with Copious Annotations and Numerous Exercises. Dublin: Hodges, Figgis, & Co.^[145] Casey produced many subsequent editions; the third edition was republished in a free online edition by Project Gutenberg. Casey's version of the Elements was likely "Casey's frost book of page torn on dirty" of the geometry section of James Joyce's Finnegans Wake.^[146] Casey also wrote A Sequel to the First Six Books of the Elements of Euclid (Dublin: Hodges, Figgis, & Co., 1881).
• Heiberg, Johan Ludvig, ed. (1883–1888) Euclidis Opera omnia [Euclid's complete works, in Greek]. Leibzig: Teubner. Volumes 1–5 comprise the Elements. Vol. I, Vol. II, Vol. III, Vol. IV, Vol. V. Heiberg consulted multiple Greek manuscripts for his work, taking the position that the single version not edited by Theon, MS. Vat.gr.190, was the most authentic, but following the others at points where he suspected his primary text to be faulty.^[81]
• Heath, Thomas, ed. (1908). The Thirteen Books of Euclid's Elements. Cambridge University Press. 2nd ed., 1926. In three volumes: Vol. I, Vol. II, Vol. III. Reprints include Dover, 1956; Green Lion Press, 2002, ISBN 1-888009-18-7 (single volume, without Heath's commentary);^[147] Barnes & Noble, 2006, ISBN 0-7607-6312-7 (single volume).

Wikiquote has quotations related to Euclid's Elements.

English Wikisource has original text related to this article:

The Elements of Euclid

Wikimedia Commons has media related to Elements of Euclid.

• Elements with highlights by ratherthanpaper
• Multilingual edition of Elementa in the Bibliotheca Polyglotta
• David E. Joyce, ed. (1997). "Euclid's Elements". In HTML with Java-based interactive figures.